![ảnh môn học Vật lí]() Vật lí
Vật lí
- SBT Vật lí Lớp 11
- Bài giảng ôn luyện kiến thức môn Vật lí lớp 11
- SGK Vật lí 11 - Chân trời sáng tạo
- Chuyên đề học tập Vật lí 11 - Chân trời sáng tạo
- SBT Vật lí 11 - Cánh Diều
- SGK Vật lí 11 - Cánh Diều
- SBT Vật lí 11 - Chân trời sáng tạo
- Tổng hợp Lí thuyết Vật lí 11
- SBT Vật lí 11 - Kết nối tri thức với cuộc sống
- SGK Vật lí 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Vật lí 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Vật lí 11 - Cánh Diều
- SGK Vật lí Nâng cao Lớp 11
- SGK Vật lí Lớp 11
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- SBT Tiếng Anh Lớp 11 mới
- Đề thi, đề kiểm tra Tiếng Anh 11 mới
- SHS Tiếng Anh 11 - Explore New Worlds
- SBT Tiếng Anh 11 - Explore New Worlds
- SBT Tiếng Anh 11 - i-Learn Smart World
- SHS Tiếng Anh 11 - English Discovery
- SBT Tiếng Anh 11 - Global Success
- SHS Tiếng Anh 11 - Bright
- SBT Tiếng Anh 11 - Friends Global
- SHS Tiếng Anh 11 - i-Learn Smart World
- SHS Tiếng Anh 11 - Global Success
- SHS Tiếng Anh 11 - Friends Global
- SBT Tiếng Anh 11 - Bright
- SBT Tiếng Anh 11 - English Discovery
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 11
- Tổng hợp Lí thuyết Tiếng Anh 11
- SGK Tiếng Anh Lớp 11 mới
- SGK Tiếng Anh Lớp 11
![ảnh môn học Sinh học]() Sinh học
Sinh học
- SBT Sinh Lớp 11
- SGK Sinh học 11 - Cánh Diều
- SBT Sinh học 11 - Cánh Diều
- SBT Sinh học 11 - Kết nối tri thức với cuộc sống
- SBT Sinh học 11 - Chân trời sáng tạo
- Chuyên đề học tập Sinh học 11 - Cánh Diều
- Chuyên đề học tập Sinh học 11 - Chân trời sáng tạo
- Chuyên đề học tập Sinh học 11 - Kết nối tri thức với cuộc sống
- Tổng hợp Lí thuyết Sinh học 11
- SGK Sinh học 11 - Kết nối tri thức với cuộc sống
- SGK Sinh học 11 - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Sinh học lớp 11
- SGK Sinh Nâng cao Lớp 11
- SGK Sinh Lớp 11
![ảnh môn học Địa lí]() Địa lí
Địa lí
- SGK Địa lí Lớp 11
- SGK Địa lí 11 - Chân trời sáng tạo
- SBT Địa lí 11 - Chân trời sáng tạo
- Chuyên đề học tập Địa lí 11 - Chân trời sáng tạo
- Tổng hợp Lí thuyết Địa lí 11
- SGK Địa lí 11 - Cánh Diều
- SBT Địa lí 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Địa lí 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Địa lí 11 - Cánh Diều
- SBT Địa lí 11 - Cánh Diều
- SGK Địa lí 11 - Kết nối tri thức với cuộc sống
- Bài giảng ôn luyện kiến thức môn Địa lí lớp 11
- SBT Địa lí Lớp 11
- Tập bản đồ Địa lí Lớp 11
![ảnh môn học Công nghệ]() Công nghệ
Công nghệ
- SGK Công nghệ Lớp 11
- SGK Công nghệ 11 - Phần Cơ khí - Cánh Diều
- SGK Công nghệ 11 - Phần Cơ khí - Chân trời sáng tạo
- SGK Công nghệ 11 - Phần Chăn nuôi - Cánh Diều
- SGK Công nghệ 11 - Phần Cơ khí - Kết nối tri thức với cuộc sống
- SGK Công nghệ 11 - Phần Chăn nuôi - Kết nối tri thức với cuộc sống
- SGK Công nghệ 11 - Phần Chăn nuôi - Chân trời sáng tạo
![ảnh môn học Hóa học]() Hóa học
Hóa học
- SGK Hóa học Nâng cao Lớp 11
- Bài giảng ôn luyện kiến thức môn Hóa học lớp 11
- SBT Hóa học 11 - Kết nối tri thức với cuộc sống
- SBT Hóa học 11 - Cánh Diều
- Chuyên đề học tập Hóa học 11 - Cánh Diều
- SGK Hóa học 11 - Kết nối tri thức với cuộc sống
- SGK Hóa học 11 - Cánh Diều
- Tổng hợp Lí thuyết Hóa học 11
- SGK Hóa học 11 - Chân trời sáng tạo
- Chuyên đề học tập Hóa học 11 - Kết nối tri thức với cuộc sống
- SBT Hóa học 11 - Chân trời sáng tạo
- Chuyên đề học tập Hóa học 11 - Chân trời sáng tạo
- SGK Hóa Lớp 11
- SBT Hóa Lớp 11
![ảnh môn học Ngữ văn]() Ngữ văn
Ngữ văn
- Soạn văn chi tiết Lớp 11
- SBT Ngữ văn 11 - Chân trời sáng tạo
- Chuyên đề học tập Ngữ văn 11 - Chân trời sáng tạo
- SBT Ngữ văn 11 - Cánh Diều
- Tuyển tập những bài văn hay Ngữ văn 11 - Chân trời sáng tạo
- SGK Ngữ văn 11 - Cánh Diều
- Chuyên đề học tập Ngữ văn 11 - Kết nối tri thức với cuộc sống
- SGK Ngữ văn 11 - Kết nối tri thức với cuộc sống
- Tuyển tập những bài văn hay Ngữ văn 11 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Ngữ Văn lớp 11
- SBT Ngữ văn 11 - Kết nối tri thức với cuộc sống
- SGK Ngữ văn 11 - Chân trời sáng tạo
- Chuyên đề học tập Ngữ văn 11 - Cánh Diều
- Tuyển tập những bài văn hay Ngữ văn 11 - Kết nối tri thức với cuộc sống
- Soạn văn siêu ngắn Lớp 11
- Tác giả - Tác phẩm Lớp 11
- Văn mẫu Lớp 11
![ảnh môn học Toán học]() Toán học
Toán học
- SBT Toán Nâng cao Lớp 11
- Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Chuyên đề học tập Toán 11 - Kết nối tri thức với cuộc sống
- SGK Toán 11 - Kết nối tri thức với cuộc sống
- SBT Toán 11 - Chân trời sáng tạo
- Chuyên đề học tập Toán 11 - Cánh Diều
- SBT Toán 11 - Cánh Diều
- SBT Toán 11 - Kết nối tri thức với cuộc sống
- SGK Toán 11 - Chân trời sáng tạo
- SGK Toán 11 - Cánh Diều
- Tổng hợp Lí thuyết Toán 11
- Bài giảng ôn luyện kiến thức môn Toán lớp 11
- SBT Toán Lớp 11
- SGK Toán Nâng cao Lớp 11
- SGK Toán Lớp 11
![ảnh môn học Lịch sử]() Lịch sử
Lịch sử
- SGK Lịch sử Lớp 11
- SGK Lịch sử 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Lịch sử 11 - Cánh Diều
- SBT Lịch sử 11 - Cánh Diều
- SBT Lịch sử 11 - Kết nối tri thức với cuộc sống
- SGK Lịch sử 11 - Chân trời sáng tạo
- Chuyên đề học tập Lịch sử 11 - Chân trời sáng tạo
- SGK Lịch sử 11 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Lịch sử lớp 11
- SBT Lịch sử 11 - Chân trời sáng tạo
- Tổng hợp Lí thuyết Lịch sử 11
- Chuyên đề học tập Lịch sử 11 - Kết nối tri thức với cuộc sống
- SBT Lịch sử Lớp 11
- Tập bản đồ Lịch sử Lớp 11
![ảnh môn học Giáo dục kinh tế và pháp luật]() Giáo dục kinh tế và pháp luật
Giáo dục kinh tế và pháp luật
- SGK Giáo dục Kinh tế và Pháp luật 11 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Giáo dục kinh tế và pháp luật lớp 11
- SBT Giáo dục Kinh tế và Pháp luật 11 - Chân trời sáng tạo
- Chuyên đề học tập Giáo dục Kinh tế và Pháp luật 11 - Cánh Diều
- SGK Giáo dục Kinh tế và Pháp luật 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Giáo dục Kinh tế và Pháp luật 11 - Chân trời sáng tạo
- Chuyên đề học tập Giáo dục Kinh tế và Pháp luật 11 - Kết nối tri thức với cuộc sống
- SGK Giáo dục Kinh tế và Pháp luật 11 - Chân trời sáng tạo
- SBT Giáo dục Kinh tế và Pháp luật 11 - Kết nối tri thức với cuộc sống
- Tổng hợp Lí thuyết Giáo dục Kinh tế và Pháp luật 11
- SBT Giáo dục Kinh tế và Pháp luật 11 - Cánh Diều
![ảnh môn học Giáo dục thể chất]() Giáo dục thể chất
Giáo dục thể chất
- SGK Giáo dục thể chất - Đá cầu - Cánh Diều
- SGK Giáo dục thể chất - Kiến thức chung - Cánh Diều
- SGK Giáo dục thể chất - Bóng chuyền - Kết nối tri thức với cuộc sống
- SGK Giáo dục thể chất - Bóng đá - Chân trời sáng tạo
- SGK Giáo dục thể chất - Bóng rổ - Kết nối tri thức với cuộc sống
- SGK Giáo dục thể chất - Bóng đá - Cánh Diều
- SGK Giáo dục thể chất - Cầu lông - Chân trời sáng tạo
- SGK Giáo dục thể chất - Bóng chuyền - Chân trời sáng tạo
- SGK Giáo dục thể chất - Bóng đá - Kết nối tri thức với cuộc sống
- SGK Giáo dục thể chất - Cầu lông - Kết nối tri thức với cuộc sống
- SGK Giáo dục thể chất - Bóng chuyền - Cánh Diều
- SGK Giáo dục thể chất - Bóng rổ - Cánh Diều
- SGK Giáo dục thể chất - Cầu lông - Cánh Diều
- SGK Giáo dục thể chất - Bóng rổ - Chân trời sáng tạo
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- Lý thuyết Tiếng Anh Lớp 10
- Đề thi, đề kiểm tra Tiếng Anh - Bright
- Đề thi, đề kiểm tra Tiếng Anh - iLearn Smart World
- Đề thi, đề kiểm tra Tiếng Anh - Global Success
- Đề thi, đề kiểm tra Tiếng Anh - English Discovery
- Đề thi, đề kiểm tra Tiếng Anh - Friends Global
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 10
- SBT Bright Lớp 10
- SBT English Discovery Lớp 10
- SBT Friends Global Lớp 10
- SBT Global Success Lớp 10
- SBT iLearn Smart World Lớp 10
- Tiếng Anh - Bright Lớp 10
- Tiếng Anh - English Discovery Lớp 10
- Tiếng Anh - Explore New Worlds Lớp 10
- Tiếng Anh - Friends Global Lớp 10
- Tiếng Anh - Global Success Lớp 10
- Tiếng Anh - iLearn Smart World Lớp 10
![ảnh môn học Lịch sử]() Lịch sử
Lịch sử
- Chuyên đề học tập Lịch sử - Kết nối tri thức Lớp 10
- Đề thi, kiểm tra Lịch sử lớp 10
- SBT Lịch sử - Cánh diều 10
- Bài giảng ôn luyện kiến thức môn Lịch sử lớp 10
- SBT Lịch sử 10 - Chân trời sáng tạo Lớp 10
- SBT Lịch sử - Kết nối tri thức Lớp 10
- SGK Lịch sử - Cánh Diều Lớp 10
- SGK Lịch sử - Chân trời sáng tạo Lớp 10
- SGK Lịch sử - Kết nối tri thức Lớp 10
![ảnh môn học Toán học]() Toán học
Toán học
- Chuyên đề học tập Toán - Cánh diều Lớp 10
- Đề thi, đề kiểm tra Toán lớp 10 - Kết nối tri thức
- Đề thi, đề kiểm tra Toán lớp 10 - Chân trời sáng tạo
- Đề thi, đề kiểm tra Toán lớp 10 - Cánh diều
- Bài giảng ôn luyện kiến thức môn Toán lớp 10
- Chuyên đề học tập Toán - Chân trời sáng tạo Lớp 10
- Chuyên đề học tập Toán - Kết nối tri thức Lớp 10
- Lý thuyết Toán Lớp 10
- SBT Toán - Cánh Diều Lớp 10
- SBT Toán - Chân trời sáng tạo Lớp 10
- SBT Toán - Kết nối tri thức Lớp 10
- SGK Toán - Cánh diều Lớp 10
- SGK Toán - Chân trời sáng tạo Lớp 10
- SGK Toán - Kết nối tri thức Lớp 10
![ảnh môn học Ngữ văn]() Ngữ văn
Ngữ văn
- Chuyên đề học tập Văn - Cánh diều Lớp 10
- Đề thi, đề kiểm tra Ngữ văn - Kết nối tri thức lớp 10
- Đề thi, đề kiểm tra Ngữ văn - Cánh diều lớp 10
- Văn mẫu - Cánh diều Lớp 10
- Văn mẫu - Kết nối tri thức
- Đề thi, đề kiểm tra Ngữ văn - Chân trời sáng tạo lớp 10
- Văn mẫu - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Ngữ Văn lớp 10
- Chuyên đề học tập Văn - Chân trời sáng tạo Lớp 10
- Chuyên đề học tập Văn - Kết nối tri thức Lớp 10
- Lý thuyết Văn Lớp 10
- SBT Văn - Cánh diều Lớp 10
- SBT Văn - Chân trời sáng tạo Lớp 10
- SBT Văn - Kết nối tri thức Lớp 10
- Soạn văn - Cánh Diều - chi tiết Lớp 10
- Soạn văn - Cánh Diều - siêu ngắn Lớp 10
- Soạn văn - Chân trời sáng tạo - chi tiết Lớp 10
- Soạn văn - Chân trời sáng tạo - siêu ngắn Lớp 10
- Soạn văn - Kết nối tri thức - chi tiết Lớp 10
- Soạn văn - Kết nối tri thức - siêu ngắn Lớp 10
- Tác giả tác phẩm Lớp 10
![ảnh môn học Sinh học]() Sinh học
Sinh học
- Chuyên đề học tập Sinh - Chân trời sáng tạo Lớp 10
- Đề thi, kiểm tra Sinh - Kết nối tri thức
- Đề thi, đề kiểm tra Sinh học 10
- Đề thi, kiểm tra Sinh - Cánh diều
- Đề thi, kiểm tra Sinh - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Sinh học lớp 10
- Chuyên đề học tập Sinh - Kết nối tri thức Lớp 10
- Lý thuyết Sinh Lớp 10
- SBT Sinh - Cánh diều Lớp 10
- SBT Sinh - Chân trời sáng tạo Lớp 10
- SBT Sinh - Kết nối tri thức Lớp 10
- SGK Sinh - Cánh diều Lớp 10
- SGK Sinh - Chân trời sáng tạo Lớp 10
- SGK Sinh - Kết nối tri thức Lớp 10
![ảnh môn học Hóa học]() Hóa học
Hóa học
- Chuyên đề học tập Hóa - Chân trời sáng tạo Lớp 10
- Đề thi, đề kiểm tra Hóa lớp 10 – Cánh diều
- Đề thi, đề kiểm tra Hóa lớp 10 – Kết nối tri thức
- Đề thi, đề kiểm tra Hóa lớp 10 – Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Hóa học lớp 10
- Chuyên đề học tập Hóa - Kết nối tri thức Lớp 10
- SBT Hóa 10 - Cánh diều Lớp 10
- SBT Hóa - Chân trời sáng tạo Lớp 10
- SBT Hóa - Kết nối tri thức Lớp 10
- SGK Hóa - Cánh diều Lớp 10
- SGK Hóa - Chân trời sáng tạo Lớp 10
- SGK Hóa - Kết nối tri thức Lớp 10
- Chuyên đề học tập Hóa - Cánh diều Lớp 10
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- SGK Tiếng Anh Lớp 8 mới
- Đề thi, đề kiểm tra Tiếng Anh 8 mới
- SHS Tiếng Anh 8 - Global Success
- SHS Tiếng Anh 8 - Explore English
- SBT Tiếng Anh 8 - Global Success
- SBT Tiếng Anh 8 - THiNK
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 8
- SBT Tiếng Anh 8 - Macmillan Motivate
- SBT Tiếng Anh 8 - Right on!
- SBT Tiếng Anh 8 - Explore English
- SBT Tiếng Anh 8 - English Discovery
- SBTTiếng Anh 8 - i-Learn Smart World
- SBT Tiếng Anh 8 - Friends Plus
- SGK Tiếng Anh Lớp 8
- SBT Tiếng Anh Lớp 8 mới
- Vở bài tập Tiếng Anh Lớp 8
![ảnh môn học GDCD]() GDCD
GDCD
- Bài tập tình huống GDCD Lớp 8
- SBT Giáo dục công dân 8 - Kết nối tri thức với cuộc sống
- SGK Giáo dục công dân 8 - Chân trời sáng tạo
- SGK Giáo dục công dân 8 - Kết nối tri thức với cuộc sống
- SBT Giáo dục công dân 8 - Chân trời sáng tạo
- Tổng hợp Lí thuyết Giáo dục công dân 8
- SGK Giáo dục công dân 8 - Cánh Diều
- SBT Giáo dục công dân 8 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Giáo dục công dân lớp 8
- SGK GDCD Lớp 8
![ảnh môn học Ngữ văn]() Ngữ văn
Ngữ văn
- Soạn văn siêu ngắn Lớp 8
- Tuyển tập những bài văn hay Ngữ văn 8 - Chân trời sáng tạo
- SBT Ngữ văn 8 - Chân trời sáng tạo
- Tuyển tập những bài văn hay Ngữ văn 8 - Kết nối tri thức với cuộc sống
- SBT Ngữ văn 8 - Kết nối tri thức với cuộc sống
- SGK Ngữ văn 8 - Cánh Diều
- VBT Ngữ văn 8 - Kết nối tri thức với cuộc sống
- Bài giảng ôn luyện kiến thức môn Ngữ Văn lớp 8
- Tổng hợp Lí thuyết Ngữ văn 8
- SGK Ngữ văn 8 - Kết nối tri thức với cuộc sống
- Tuyển tập những bài văn hay Ngữ văn 8 - Cánh Diều
- SGK Ngữ văn 8 - Chân trời sáng tạo
- SBT Ngữ văn 8 - Cánh Diều
- Soạn văn chi tiết Lớp 8
- Tác giả - Tác phẩm văn Lớp 8
- Văn mẫu Lớp 8
- Vở bài tập Ngữ văn Lớp 8
![ảnh môn học Toán học]() Toán học
Toán học
- SGK Toán Lớp 8
- SGK Toán 8 - Chân trời sáng tạo
- SBT Toán 8 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Toán lớp 8
- SGK Toán 8 - Cánh Diều
- VBT Toán 8 - Kết nối tri thức với cuộc sống
- SBT Toán 8 - Kết nối tri thức với cuộc sống
- SGK Toán 8 - Kết nối tri thức với cuộc sống
- Tổng hợp Lí thuyết Toán 8
- SBT Toán Lớp 8
- Giải bài tập Toán Lớp 8
- Tài liệu Dạy - học Toán Lớp 8
- Đề thi, đề kiểm tra Toán Lớp 8
![ảnh môn học Lịch sử và Địa lí]() Lịch sử và Địa lí
Lịch sử và Địa lí
- Bài giảng ôn luyện kiến thức môn Địa lí lớp 8
- SGK Lịch sử và Địa lí 8 - Chân trời sáng tạo
- SBT Lịch sử và Địa lí 8 - Chân trời sáng tạo
- SBT Lịch sử và Địa lí 8 - Kết nối tri thức với cuộc sống
- SGK Lịch sử và Địa lí 8 - Cánh Diều
- SBT Lịch sử và Địa lí 8 - Cánh Diều
- SGK Lịch sử và Địa lí 8 - Kết nối tri thức với cuộc sống 1
- Tổng hợp Lí thuyết Lịch sử và Địa lí 8
- Bài giảng ôn luyện kiến thức môn Lịch sử lớp 8
![ảnh môn học Khoa học tự nhiên]() Khoa học tự nhiên
Khoa học tự nhiên
- SGK Khoa học tự nhiên 8 - Kết nối tri thức với cuộc sống
- SGK Khoa học tự nhiên 8 - Cánh Diều
- SBT Khoa học tự nhiên 8 - Chân trời sáng tạo
- SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- SBT Khoa học tự nhiên 8 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Khoa học tự nhiên lớp 8
- Tổng hợp Lí thuyết Khoa học tự nhiên 8
- SBT Khoa học tự nhiên 8 - Kết nối tri thức với cuộc sống
![ảnh môn học Khoa học tự nhiên]() Khoa học tự nhiên
Khoa học tự nhiên
- Lý thuyết Khoa học tự nhiên Lớp 7
- Đề thi, đề kiểm tra KHTN - Kết nối tri thức
- Đề thi, đề kiểm tra KHTN - Chân trời sáng tạo
- Đề thi, đề kiểm tra KHTN - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Khoa học tự nhiên lớp 7
- SBT KHTN - Cánh diều Lớp 7
- SBT KHTN - Chân trời sáng tạo Lớp 7
- SBT KHTN - Kết nối tri thức Lớp 7
- SGK Khoa học tự nhiên - Cánh diều Lớp 7
- SGK Khoa học tự nhiên - Chân trời sáng tạo Lớp 7
- SGK Khoa học tự nhiên - Kết nối tri thức Lớp 7
- Vở thực hành Khoa học tự nhiên Lớp 7
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- Lý thuyết Tiếng Anh Lớp 7
- Đề thi, đề kiểm tra Tiếng Anh - Right on!
- Đề thi, đề kiểm tra Tiếng Anh - English Discovery
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 7
- SBT English Discovery Lớp 7
- SBT Friends Plus Lớp 7
- SBT Global Success Lớp 7
- SBT iLearn Smart World Lớp 7
- SBT Right on! Lớp 7
- Tiếng Anh - English Discovery Lớp 7
- Tiếng Anh - Friends Plus Lớp 7
- Tiếng Anh - iLearn Smart World Lớp 7
- Tiếng Anh - Right on! Lớp 7
- Tiếng Anh - Global Success Lớp 7
- Đề thi, đề kiểm tra Tiếng Anh - Friends Plus
- Đề thi, đề kiểm tra Tiếng Anh - Global Success
- Đề thi, đề kiểm tra Tiếng Anh - iLearn Smart World
![ảnh môn học Lịch sử và Địa lí]() Lịch sử và Địa lí
Lịch sử và Địa lí
- SBT Lịch sử và Địa lí - Chân trời sáng tạo Lớp 7
- SBT Lịch sử và Địa lí - Cánh diều lớp 7
- Bài giảng ôn luyện kiến thức môn Địa lí lớp 7
- Bài giảng ôn luyện kiến thức môn Lịch sử lớp 7
- SBT Lịch sử và Địa lí - Kết nối tri thức Lớp 7
- SGK Lịch sử và Địa lí - Cánh Diều Lớp 7
- SGK Lịch sử và Địa lí - Chân trời sáng tạo Lớp 7
- SGK Lịch sử và Địa lí - Kết nối tri thức Lớp 7
![ảnh môn học Ngữ văn]() Ngữ văn
Ngữ văn
- Đề thi, đề kiểm tra Văn - Cánh diều Lớp 7
- Bài tập trắc nghiệm Văn 7 - Kết nối tri thức
- Bài tập trắc nghiệm Văn 7 - Cánh diều
- Bài tập trắc nghiệm Văn 7 - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Ngữ Văn lớp 7
- Đề thi, đề kiểm tra Văn - Chân trời sáng tạo Lớp 7
- Đề thi, đề kiểm tra Văn - Kết nối tri thức Lớp 7
- Lý thuyết Văn Lớp 7
- SBT Văn - Cánh diều Lớp 7
- SBT Văn - Chân trời sáng tạo Lớp 7
- SBT Văn - Kết nối tri thức Lớp 7
- Soạn văn chi tiết - Cánh diều Lớp 7
- Soạn văn siêu ngắn - Cánh diều Lớp 7
- Soạn văn chi tiết - CTST Lớp 7
- Soạn văn siêu ngắn - CTST Lớp 7
- Soạn văn chi tiết - KNTT Lớp 7
- Soạn văn siêu ngắn - KNTT Lớp 7
- Tác giả - Tác phẩm văn Lớp 7
- Văn mẫu - Cánh Diều Lớp 7
- Văn mẫu - Chân trời sáng tạo Lớp 7
- Văn mẫu - Kết nối tri thức Lớp 7
- Vở thực hành văn Lớp 7
![ảnh môn học Toán học]() Toán học
Toán học
- Đề thi, đề kiểm tra Toán - Chân trời sáng tạo Lớp 7
- Bài tập trắc nghiệm Toán - Kết nối tri thức
- Đề thi, đề kiểm tra Toán - Cánh diều Lớp 7
- Bài tập trắc nghiệm Toán - Cánh diều
- Đề thi, đề kiểm tra Toán - Kết nối tri thức Lớp 7
- Bài tập trắc nghiệm Toán - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Toán lớp 7
- Lý thuyết Toán Lớp 7
- SBT Toán - Cánh diều Lớp 7
- SBT Toán - Chân trời sáng tạo Lớp 7
- SBT Toán - Kết nối tri thức Lớp 7
- SGK Toán - Cánh diều Lớp 7
- SGK Toán - Chân trời sáng tạo Lớp 7
- SGK Toán - Kết nối tri thức Lớp 7
- Tài liệu Dạy - học Toán Lớp 7
- Vở thực hành Toán Lớp 7
![ảnh môn học Toán học]() Toán học
Toán học
- SGK Toán Lớp 5
- Bài tập trắc nghiệm Toán 5
- Công thức Toán lớp 5
- Toán nâng cao lớp 5
- Bài giảng ôn luyện kiến thức môn Toán lớp 5
- Kết nối tri thức
- VNEN Toán Lớp 5
- Vở bài tập Toán Lớp 5
- Bài tập cuối tuần Toán Lớp 5
- Cùng em học toán Lớp 5
- Đề thi, đề kiểm tra Toán Lớp 5
- Bài tập phát triển năng lực Toán Lớp 5
![ảnh môn học Lịch sử và Địa lí]() Lịch sử và Địa lí
Lịch sử và Địa lí
- SGK Lịch sử và Địa lí Lớp 4
- SGK Lịch sử và Địa lí 4 - Cánh Diều
- VBT Lịch sử và Địa lí 4 - Chân trời sáng tạo
- SGK Lịch sử và Địa lí 4 - Kết nối tri thức với cuộc sống
- VBT Lịch sử và Địa lí 4 - Cánh Diều
- SGK Lịch sử và Địa lí 4 - Chân trời sáng tạo
- VBT Lịch sử và Địa lí 4 - Kết nối tri thức với cuộc sống
- Vở bài tập Lịch sử Lớp 4
- Vở bài tập Địa lí Lớp 4
![ảnh môn học Toán học]() Toán học
Toán học
- SGK Toán Lớp 4
- SGK Toán 4 - Kết nối tri thức với cuộc sống
- STK - Cùng em phát triển năng lực Toán 4
- Bài giảng ôn luyện kiến thức môn Toán lớp 4
- SGK Toán 4 - Chân trời sáng tạo
- SGK Toán 4 - Cánh Diều
- VBT Toán 4 - Chân trời sáng tạo
- VBT Toán 4 - Kết nối tri thức với cuộc sống
- VBT Toán 4 - Cánh Diều
- VNEN Toán Lớp 4
- Vở bài tập Toán Lớp 4
- Bài tập cuối tuần Toán Lớp 4
- Cùng em học toán Lớp 4
- Ôn tập hè Toán Lớp 4
- Đề thi, đề kiểm tra Toán Lớp 4
- Bài tập phát triển năng lực Toán Lớp 4
![ảnh môn học Tiếng việt]() Tiếng việt
Tiếng việt
- SGK Tiếng Việt Lớp 4
- VBT Tiếng Việt 4 - Cánh Diều
- SGK Tiếng Việt 4 - Chân trời sáng tạo
- VBT Tiếng Việt 4 - Chân trời sáng tạo
- SGK Tiếng Việt 4 - Kết nối tri thức với cuộc sống
- VBT Tiếng Việt 4 - Kết nối tri thức với cuộc sống
- SGK Tiếng Việt 4 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Tiếng Việt lớp 4
- Cùng em học Tiếng Việt Lớp 4
- VNEN Tiếng Việt Lớp 4
- Vở bài tập Tiếng Việt Lớp 4
- Văn mẫu Lớp 4
- Đề thi, đề kiểm tra Tiếng Việt Lớp 4
- Ôn tập hè Tiếng Việt Lớp 4
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- SGK Tiếng Anh Lớp 4 Mới
- Đề thi, đề kiểm tra Tiếng Anh lớp 4
- SHS Tiếng Anh 4 - Family and Friends
- SHS Tiếng Anh 4 - i-Learn Smart Start
- SBT Tiếng Anh 4 - Explore Our World
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 4
- SBT Tiếng Anh 4 - i-Learn Smart Start
- SHS Tiếng Anh 4 - Phonics-Smart
- SBT Tiếng Anh 4 - Global Success
- SHS Tiếng Anh 4 - Explore Our World
- SBT Tiếng Anh 4 - Phonics-Smart
- SHS Tiếng Anh 4 - Global Success
- SBT Tiếng Anh 4 - Family and Friends
- SBT Tiếng Anh Lớp 4
- Ôn tập hè Tiếng Anh Lớp 4
![ảnh môn học Toán học]() Toán học
Toán học
- Bài tập cuối tuần môn Toán Lớp 3
- Bài tập trắc nghiệm Toán - Kết nối tri thức
- Đề thi, đề kiểm tra Toán - Chân trời sáng tạo
- Bài tập trắc nghiệm Toán - Chân trời sáng tạo
- Bài tập trắc nghiệm Toán - Cánh diều
- Đề thi, đề kiểm tra Toán - Kết nối tri thức
- Đề thi, đề kiểm tra Toán - Cánh diều
- Bài giảng ôn luyện kiến thức môn Toán lớp 3
- Cùng em học Toán Lớp 3
- SGK Toán - Cánh diều Lớp 3
- SGK Toán - Chân trời sáng tạo Lớp 3
- SGK Toán - Kết nối tri thức Lớp 3
- VBT Toán - Kết nối tri thức Lớp 3
![ảnh môn học Tiếng việt]() Tiếng việt
Tiếng việt
- Cùng em học Tiếng Việt Lớp 3
- VBT Tiếng Việt - Cánh diều Lớp 3
- Đề thi, đề kiểm tra Tiếng Việt 3
- Bài giảng ôn luyện kiến thức môn Tiếng Việt lớp 3
- Tiếng Việt - Cánh diều Lớp 3
- Tiếng Việt - Chân trời sáng tạo Lớp 3
- Tiếng Việt - Kết nối tri thức Lớp 3
- Văn mẫu - Kết nối tri thức Lớp 3
- Văn mẫu Lớp 3
- VBT Tiếng Việt - Chân trời sáng tạo Lớp 3
- VBT Tiếng Việt - Kết nối tri thức Lớp 3
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- Bài tập trắc nghiệm Tiếng Anh - Family and Friends
- Đề thi, đề kiểm tra Tiếng Anh - Family and Friends Lớp 3
- Bài tập trắc nghiệm Tiếng Anh - iLearn Smart Start
- Bài tập trắc nghiệm Tiếng Anh - Global Success
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 3
- Đề thi, đề kiểm tra Tiếng Anh - Global Success Lớp 3
- Đề thi, đề kiểm tra Tiếng Anh - iLearn Smart Start Lớp 3
- SBT Tiếng Anh - Family and Friends Lớp 3
- SBT Tiếng Anh - iLearn Smart Start Lớp 3
- SBT Tiếng Anh - Global Success Lớp 3
- SBT Tiếng Anh - Phonics Smart Lớp 3
- Tiếng Anh 3 - Explore Our World Lớp 3
- Tiếng Anh - Family and Friends Lớp 3
- Đề thi, đề kiểm tra Tiếng Anh - Explore Our World
- Tiếng Anh - Global Success Lớp 3
- Tiếng Anh - iLearn Smart Start Lớp 3
- Đề thi, đề kiểm tra Tiếng Anh - Phonics Smart
- Tiếng Anh 3 - Phonics Smart Lớp 3
![ảnh môn học Tiếng việt]() Tiếng việt
Tiếng việt
- Tiếng Việt - Kết nối tri thức Lớp 2
- Bài giảng ôn luyện kiến thức môn Tiếng Việt lớp 2
- Tiếng Việt - Chân trời sáng tạo Lớp 2
- Tiếng Việt - Cánh Diều Lớp 2
- Văn mẫu - Kết nối tri thức Lớp 2
- Văn mẫu - Chân trời sáng tạo Lớp 2
- Văn mẫu - Cánh diều Lớp 2
- VBT Tiếng Việt - Kết nối tri thức Lớp 2
- VBT Tiếng Việt - Chân trời sáng tạo Lớp 2
- VBT Tiếng Việt - Cánh diều Lớp 2
- Cùng em học Tiếng Việt Lớp 2
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- Tiếng Anh - Kết nối tri thức Lớp 2
- Đề thi, đề kiểm tra Tiếng Anh - Global Success
- Đề thi, đề kiểm tra Tiếng Anh - iLearn Smart Start
- Đề thi, đề kiểm tra Tiếng Anh - Phonics Smart
- Đề thi, đề kiểm tra Tiếng Anh - English Discovery
- Đề thi, đề kiểm tra Tiếng Anh - Family and Friends
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 2
- Tiếng Anh - Family and Friends Lớp 2
- Tiếng Anh - iLearn Smart Start Lớp 2
- Tiếng Anh - Phonics Smart Lớp 2
- Tiếng Anh - English Discovery Lớp 2
- Tiếng Anh - Explore Our World Lớp 2
- Family & Friends Special Grade Lớp 2
- SBT Kết nối tri thức Lớp 2
- SBT Family and Friends Lớp 2
- SBT iLearn Smart Start Lớp 2
- SBT Phonics Smart Lớp 2
- SBT English Discovery Lớp 2
- SBT Explore Our World Lớp 2
![ảnh môn học Toán học]() Toán học
Toán học
- SGK Toán - Kết nối tri thức Lớp 2
- Bài tập trắc nghiệm Toán - Kết nối tri thức
- Bài tập trắc nghiệm Toán - Cánh diều
- Đề thi, đề kiểm tra Toán - Chân trời sáng tạo
- Đề thi, đề kiểm tra Toán - Kết nối tri thức
- Đề thi, đề kiểm tra Toán - Cánh diều
- Bài tập trắc nghiệm Toán - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Toán lớp 2
- SGK Toán - Chân trời sáng tạo Lớp 2
- SGK Toán - Cánh Diều Lớp 2
- VBT Toán - KNTT Lớp 2
- VBT Toán - CTST Lớp 2
- Cùng em học Toán 2
- Bài tập cuối tuần Toán Lớp 2
- Ôn tập hè Tiếng Anh lớp 6
- Bài tập trắc nghiệm Tiếng Anh - iLearn Smart World
- Bài tập trắc nghiệm Tiếng Anh 6 - English Discovery
- Bài tập trắc nghiệm Tiếng Anh - Friends Plus
- Bài tập trắc nghiệm Tiếng Anh - Global Success
- Bài tập trắc nghiệm Tiếng Anh - Right on!
- SBT Global Success Lớp 6
- SBT English Discovery Lớp 6
- SBT Friends Plus Lớp 6
- SBT iLearn Smart World Lớp 6
- SBT Right on! Lớp 6
- Tiếng Anh - Explore English Lớp 6
- Tiếng Anh - Friends plus Lớp 6
- Tiếng Anh - English Discovery Lớp 6
- Global Success (Pearson) Lớp 6
- Tiếng Anh - iLearn Smart World Lớp 6
- Tiếng Anh - Right on Lớp 6
- Đề thi, đề kiểm tra Tiếng Anh - English Discovery
- Đề thi, đề kiểm tra Tiếng Anh - Friends Plus
- Đề thi, đề kiểm tra Tiếng Anh - iLearn Smart World
- Đề thi, đề kiểm tra Tiếng Anh - Global Success
- Đề thi, đề kiểm tra Tiếng Anh - Right on!
- SGK KHTN - Cánh Diều Lớp 6
- Đề thi, đề kiểm tra KHTN - Kết nối tri thức
- Đề thi, đề kiểm tra KHTN - Chân trời sáng tạo
- Đề thi, đề kiểm tra KHTN - Cánh diều
- Bài giảng ôn luyện kiến thức môn Khoa học tự nhiên lớp 6
- SGK KHTN - Chân trời sáng tạo Lớp 6
- SGK KHTN - Kết nối tri thức Lớp 6
- SBT KHTN - Cánh Diều Lớp 6
- SBT KHTN - Chân trời sáng tạo Lớp 6
- SBT KHTN - Kết nối tri thức Lớp 6
- Vở thực hành Khoa học tự nhiên Lớp 6
- SGK Trải nghiệm, hướng nghiệp - Cánh diều Lớp 6
- SGK Trải nghiệm, hướng nghiệp - Chân trời sáng tạo Lớp 6
- SGK Trải nghiệm, hướng nghiệp - Kết nối tri thức Lớp 6
- SBT Trải nghiệm, hướng nghiệp - Chân trời sáng tạo Lớp 6
- SBT Trải nghiệm, hướng nghiệp - Kết nối tri thức Lớp 6
- Thực hành Trải nghiệm, hướng nghiệp - Cánh diều Lớp 6
- SGK Lịch sử và Địa lí - Cánh Diều Lớp 6
- Đề thi, kiểm tra Lịch sử và Địa lí - Kết nối tri thức
- Đề thi, kiểm tra Lịch sử và Địa lí - Cánh Diều
- Đề thi, kiểm tra Lịch sử và Địa lí - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Địa lí lớp 6
- Bài giảng ôn luyện kiến thức môn Lịch sử lớp 6
- SGK Lịch sử và Địa lí - CTST Lớp 6
- SGK Lịch sử và Địa lí - KNTT Lớp 6
- SBT Lịch sử và Địa lí - KNTT Lớp 6
- SBT Lịch sử và Địa lí - Cánh diều Lớp 6
- SBT Lịch sử và Địa lí - CTST Lớp 6
- Đề thi, đề kiểm tra Văn - Cánh diều Lớp 6
- Bài tập trắc nghiệm Văn - Kết nối tri thức
- Bài tập trắc nghiệm Văn - Chân trời sáng tạo
- Đề thi, đề kiểm tra Văn - Kết nối tri thức
- Bài tập trắc nghiệm Văn - Cánh diều
- Bài giảng ôn luyện kiến thức môn Ngữ Văn lớp 6
- Đề thi, đề kiểm tra Văn - Chân trời sáng tạo Lớp 6
- Đề thi, đề kiểm tra Văn - Kết nối tri thức Lớp 6
- SBT Văn - Chân trời sáng tạo Lớp 6
- Ôn tập hè Văn Lớp 6
- SBT Văn - Cánh diều Lớp 6
- SBT Văn - Kết nối tri thức Lớp 6
- Soạn văn chi tiết - Cánh diều Lớp 6
- Soạn văn siêu ngắn - Cánh diều Lớp 6
- Soạn văn chi tiết - CTST Lớp 6
- Soạn văn siêu ngắn - CTST Lớp 6
- Soạn văn chi tiết - KNTT Lớp 6
- Soạn văn siêu ngắn - KNTT Lớp 6
- Tác giả - Tác phẩm văn Lớp 6
- Văn mẫu - Cánh Diều Lớp 6
- Văn mẫu - Kết nối tri thức Lớp 6
- Văn mẫu - Chân trời sáng tạo Lớp 6
- Vở thực hành văn Lớp 6
- Ôn tập hè Toán Lớp 6
- Bài tập trắc nghiệm Toán - Cánh diều
- Bài tập trắc nghiệm Toán - Kết nối tri thức
- Bài tập trắc nghiệm Toán 6 - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Toán lớp 6
- SBT Toán - Cánh diều Lớp 6
- SBT Toán - Kết nối tri thức Lớp 6
- SBT Toán - Chân trời sáng tạo Lớp 6
- Tài liệu Dạy - học Toán Lớp 6
- SGK Toán - Cánh diều Lớp 6
- SGK Toán - Chân trời sáng tạo Lớp 6
- SGK Toán - Kết nối tri thức Lớp 6
- Đề thi, đề kiểm tra Toán - Cánh diều
- Đề thi, đề kiểm tra Toán - Chân trời sáng tạo
- Đề thi, đề kiểm tra Toán - Kết nối tri thức
- Vở thực hành Toán Lớp 6
Đề kiểm tra giữa học kì 2 Toán 6 - Đề số 4 - Cánh diều
Đề bài
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
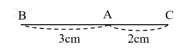
Câu 1: Cho hình vẽ, đoạn thẳng BC có độ dài bằng:
A. 3cm B. 2cm C. 4cm D. 5cm
Câu 2: Khi điều tra về một vấn đề nào đó, người ta thường thu thập dữ liệu và ghi lại trong
A. bảng tần số B. bảng dữ liệu ban đầu C. bảng thời gian D. bảng số liệu
Câu 3: Kết quả phép tính \(\dfrac{1}{5} - \dfrac{1}{4} + \dfrac{1}{{20}}\) là :
A.\(10\) B.\(0\) C.\(\dfrac{{ - 1}}{{10}}\) D.\(\dfrac{1}{{10}}\)
Câu 4: Trên tia \(Ax\) lấy hai điểm \(B\) và \(C\) sao cho \(AC = 3cm,\,\,AB = 8cm\). Khi đó độ dài của đoạn thẳng \(BC\) bằng
A. \(11\) B. \(11cm\) C. \(5\) D. \(5cm\)
Phần II. Tự luận (8 điểm):
Bài 1: (1,5 điểm) Thực hiện phép tính:
\(a)\,\dfrac{{ - 7}}{9} + \dfrac{5}{{12}} - \dfrac{{11}}{{18}}\) \(b)\,2\dfrac{2}{7}:\dfrac{{ - 32}}{{35}}\) \(c)\,\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{8}{{19}}.\dfrac{{ - 7}}{{11}} + \dfrac{{ - 4}}{{11}}\)
Bài 2 (1,5 điểm) Tìm \(x\):
\(a)\,x + \dfrac{7}{9} = - \dfrac{5}{6}\) \(b)\,x:\dfrac{{ - 21}}{{20}} = 2\dfrac{1}{7}\) \(c)\,\dfrac{5}{6}x - 1 = - \dfrac{2}{3}\)
Bài 3 (2 điểm) Cho biểu đồ cột kép sau:

a) Năm 2019, dân số Hà Nội là bao nhiêu người? Bao nhiêu người ở thành thị, bao nhiêu người ở nông thôn?
b) Có bao nhiêu tỉnh, thành phố có số dân ở nông thôn lớn hơn số dân ở thành thị? Đó là những tỉnh, thành phố nào?
c) Lập bảng thống kê tổng số dân của các tỉnh, thành phố?
Bài 4: (2,5 điểm) Trên tia Ox lấy hai điểm A và B sao cho OA = 3cm, OB = 7cm.
a) Trong ba điểm O, A, B điểm nào nằm giữa hai điểm còn lại? Vì sao?
b) Tính độ dài đoạn thẳng AB.
c) Gọi H là trung điểm của OA. Tính độ dài đoạn thẳng HB.
Bài 5: (0,5 điểm) Tìm \(x\) , biết: \(\dfrac{1}{{2.4}} + \dfrac{1}{{4.6}} + \cdot \cdot \cdot + \dfrac{1}{{(2x - 2).2x}} = \dfrac{1}{8}\,\,\,\,\,\,\,\,\,\,\,\,\,(x \in \mathbb{N},\,\,x \ge 2)\)
Lời giải
Phần I: Trắc nghiệm
1. D | 2. B | 3. B | 4. D |
Câu 1
Phương pháp:
\(BC = AB + AC\)
Cách giải:
Vì A nằm giữa B và C nên \(BC = AB + AC\)
Vậy độ dài đoạn thẳng BC là: \(3 + 2 = 5\left( {cm} \right)\)
Chọn D.
Câu 2
Phương pháp:
Sử dụng lý thuyết bảng dữ liệu ban đầu.
Cách giải:
Khi điều tra về một vấn đề nào đó, người ta thường thu thập dữ liệu và ghi lại trong bảng dữ liệu ban đầu.
Chọn B.
Câu 3
Phương pháp:
Quy đồng mẫu các phân số rồi thực hiện cộng các phân số cùng mẫu với nhau.
Quy đồng mẫu số nhiều phân số với mẫu dương ta làm như sau :
Bước 1 : Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.
Bước 2 : Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu)
Bước 3 : Nhân tử và mẫu của phân số với thừa số phụ tương ứng.
Cách giải :
\(\dfrac{1}{5} - \dfrac{1}{4} + \dfrac{1}{{20}} = \dfrac{4}{{20}} - \dfrac{5}{{20}} + \dfrac{1}{{20}} = \dfrac{{4 - 5 + 1}}{{20}} = 0\)
Chọn B
Câu 4
- Áp dụng nhận xét: Trên tia\(Ox,{\rm{ }}OM = a,{\rm{ }}ON = b\) , nếu \(0 < a < b\) thì điểm \(M\) nằm giữa hai điểm \(O\) và \(N\).
- Áp dụng tính chất: Nếu điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) thì\(AM + MB = AB\).
Cách giải:
Trên tia \(Ax\) ta có \(AC < AB\,\,\left( {do\,\,3cm < 8cm} \right)\) nên điểm \(C\) là điểm nằm giữa hai điểm \(A\) và \(B\)
\(\begin{array}{l} \Rightarrow AC + CB = AB\\ \Rightarrow CB = AB - AC = 8 - 3 = 5\,\,\left( {cm} \right)\end{array}\)
Vậy độ dài đoạn thẳng \(BC\) là \(5cm\).
Chọn D.
Phần II: Tự luận
Bài 1
Phương pháp
a) Viết ba phân số về cùng mẫu số rồi thực hiện phép tính cộng các phân số cùng mẫu số: ta cộng tử với tử mẫu giữ nguyên: \(\dfrac{a}{m} + \dfrac{b}{m} + \dfrac{c}{m} = \dfrac{{a + b + c}}{m}\)
b) Chuyển hỗn số về phân số rồi thực hiện chia hai phân số: \(\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c}\)
c) Nhóm \(\left( {\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{{ - 7}}{{11}}.\dfrac{8}{{19}}} \right) + \dfrac{{ - 4}}{{11}}\) , rồi thực hiện phép tính trong ngoặc trước. Để thực hiện phép tính trong ngoặc ta biến đổi chúng thành một số nhân với một tổng: \(\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{{ - 7}}{{11}}.\dfrac{8}{{19}} = \dfrac{{ - 7}}{{11}}.\left( {\dfrac{{11}}{{19}} + \dfrac{8}{{11}}} \right)\)
Kiến thức sử dụng: Tính chất phân phối của phép nhân đối với phép cộng: \(a.b + a.c = a.\left( {b + c} \right)\)
Cách giải:
\(\begin{array}{l}a)\,\dfrac{{ - 7}}{9} + \dfrac{5}{{12}} - \dfrac{{11}}{{18}}\\ = \dfrac{{ - 7.4}}{{36}} + \dfrac{{5.3}}{{36}} - \dfrac{{11.2}}{{36}}\\ = \dfrac{{ - 28}}{{36}} + \dfrac{{15}}{{36}} - \dfrac{{22}}{{36}}\\ = \dfrac{{ - 28 + 15 - 22}}{{36}}\\ = \dfrac{{ - 35}}{{36}}\end{array}\)
\(b)\,2\dfrac{2}{7}:\dfrac{{ - 32}}{{35}} = \dfrac{{16}}{7}:\dfrac{{ - 32}}{{35}} = \dfrac{{16}}{7}.\dfrac{{ - 35}}{{32}} = \dfrac{{ - 5}}{2}\)
\(\begin{array}{l}c)\,\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{8}{{19}}.\dfrac{{ - 7}}{{11}} + \dfrac{{ - 4}}{{11}} = \left( {\dfrac{{ - 7}}{{11}}.\dfrac{{11}}{{19}} + \dfrac{8}{{19}}.\dfrac{{ - 7}}{{11}}} \right) + \dfrac{{ - 4}}{{11}}\\ = \dfrac{{ - 7}}{{11}}.\left( {\dfrac{{11}}{{19}} + \dfrac{8}{{19}}} \right) + \dfrac{{ - 4}}{{11}}\\ = \dfrac{{ - 7}}{{11}}.1 + \dfrac{{ - 4}}{{11}}\\ = \dfrac{{ - 11}}{{11}}\\ = - 1\end{array}\)
Bài 2:
Phương pháp:
a) Chuyển \(\dfrac{7}{9}\) từ vế trái sang vế phải đổi dấu thành \(\dfrac{{ - 7}}{9}\) , rồi thực hiện phép tính ở bên vế phải, ta tìm được x.
b) Chuyển hỗn số về dạng phân số. Để tìm x ta nhân phân số ở bên vế phải với \(\dfrac{{ - 21}}{{20}}\).
c) Chuyển \( - 1\) ở vế trái sang vế phải đổi dấu thành \( + 1\) rồi thực hiện phép tính bên vế phải. Để tìm x ta lấy kết quả phép tính vừa tính bên vế phải chia cho \(\dfrac{5}{6}\).
Cách giải:
\(\begin{array}{l}a)\,x + \dfrac{7}{9} = - \dfrac{5}{6}\\\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\, = \dfrac{{ - 5}}{6} - \dfrac{7}{9}\\\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\, = \dfrac{{ - 15}}{{18}} - \dfrac{{14}}{{18}}\\\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\, = \,\dfrac{{ - 29}}{{18}}\end{array}\)
Vậy \(x = \dfrac{{ - 29}}{{18}}\)
\(\begin{array}{l}b)\,x:\dfrac{{ - 21}}{{20}}\,\,\, = 2\dfrac{1}{7}\\\,\,\,\,\,x:\dfrac{{ - 21}}{{20}}\,\,\, = \dfrac{{15}}{7}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{15}}{7}.\dfrac{{ - 21}}{{20}}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{3.5}}{7}.\dfrac{{\left( { - 3} \right).7}}{{4.5}}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 9}}{4}\end{array}\)
Vậy \(x = \dfrac{{ - 9}}{4}\)
\(\begin{array}{l}c)\,\dfrac{5}{6}x - 1 = - \dfrac{2}{3}\\\,\,\,\,\dfrac{5}{6}x\,\,\,\,\,\,\,\,\, = \dfrac{{ - 2}}{3} + 1\\\,\,\,\,\,\dfrac{5}{6}x\,\,\,\,\,\,\,\, = \dfrac{1}{3}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\, = \dfrac{1}{3}:\dfrac{5}{6}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{6}{5}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\, = \dfrac{2}{5}\end{array}\)
Vậy \(x = \dfrac{2}{5}\)
Bài 3
Phương pháp:
Sử dụng lý thuyết biểu đồ cột kép.
Cách giải:
a) Năm 2019, số dân Hà Nội là 8 093 000 người gồm 4 000 000 người ở thành thị và 4 093 000 người ở nông thôn.
b) Có 5 tỉnh, thành phố có số dân ở nông thôn lớn hơn ở thành thị gồm Hà Nội, Hải Phòng, Hưng Yên, Hà Giang, Bắc Kạn.
c) Với mỗi tỉnh, thành phố, tính tổng số dân bằng cách cộng số dân ở thành thị với số dân ở nông thôn ta được bảng thống kê sau:
Tỉnh, thành phố | Hà Nội | Hải Phòng | Hưng Yên | Hà Giang | Bắc Kạn | Đà Nẵng |
Số dân (nghìn người) | 8 093 | 2 033 | 1 256 | 858 | 315 | 1 142 |
Bài 4
Phương pháp:
a) Vẽ hình, so sánh độ dài hai đoạn OA và OB.
b) Áp dụng tính chất của điểm nằm giữa hai điểm.
c) Áp dụng tính chất của trung điểm của đoạn thẳng.
Cách giải:

a)
Vì A và B nằm cùng phía so với điểm O mà OA < OB
Nên điểm A nằm giữa hai điểm O và B.
b)
Vì điểm A nằm giữa hai điểm O và B nên ta có: \(OA + AB = OB\)
Hay \(3 + AB = 7\)
Suy ra: \(AB = 7 - 3 = 4\left( {cm} \right)\)
c)
Vì H là trung điểm của đoạn thẳng OA nên \(HA = \dfrac{{OA}}{2} = \dfrac{4}{2} = 2\left( {{\rm{cm}}} \right)\)
Vì A nằm giữa H và B nên \(HB = HA + AB = 2 + 4 = 6\left( {{\rm{cm}}} \right)\)
Bài 5
Phương pháp:
Thu gọn vế trái rồi tìm \(x\).
Cách giải:
Ta có:
\(\begin{array}{l}\dfrac{1}{{2.4}} + \dfrac{1}{{4.6}} + \cdot \cdot \cdot + \dfrac{1}{{(2x - 2).2x}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{8}\\\dfrac{1}{2}.\left( {\dfrac{1}{2} - \dfrac{1}{4} + \dfrac{1}{4} - \dfrac{1}{6} + \cdot \cdot \cdot + \dfrac{1}{{(2x - 2)}} - \dfrac{1}{{2x}}} \right) = \dfrac{1}{8}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{2}.\left( {\dfrac{1}{2} - \dfrac{1}{{2x}}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{8}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{2} - \dfrac{1}{{2x}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{8}:\dfrac{1}{2}\end{array}\)
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{2} - \dfrac{1}{{2x}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{{2x}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2} - \dfrac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{{2x}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{4}\\ \Rightarrow 2x = 4\\ \Rightarrow \,x\, = 2\end{array}\)
Vậy \(x = 2\).
Gợi ý sách
Chủ đề 4. NUÔI DƯỠNG QUAN HỆ GIA ĐÌNH
Chủ đề IV - ĐỒ DÙNG ĐIỆN TRONG GIA ĐÌNH
Unit 4: Holidays!
Bài giảng ôn luyện kiến thức giữa học kì 1 môn Địa lí lớp 6
Chương 8. Hình học phẳng. Các hình hình học cơ bản

Bộ sách liên quan
Ôn tập hè Toán Lớp 6
Bài tập trắc nghiệm Toán - Cánh diều
Bài tập trắc nghiệm Toán - Kết nối tri thức
Bài tập trắc nghiệm Toán 6 - Chân trời sáng tạo
Bài giảng ôn luyện kiến thức môn Toán lớp 6
SBT Toán - Cánh diều Lớp 6
SBT Toán - Kết nối tri thức Lớp 6
SBT Toán - Chân trời sáng tạo Lớp 6
Tài liệu Dạy - học Toán Lớp 6
SGK Toán - Cánh diều Lớp 6
SGK Toán - Chân trời sáng tạo Lớp 6
SGK Toán - Kết nối tri thức Lớp 6
Đề thi, đề kiểm tra Toán - Chân trời sáng tạo
Đề thi, đề kiểm tra Toán - Kết nối tri thức
Vở thực hành Toán Lớp 6