![ảnh môn học Vật lí]() Vật lí
Vật lí
- SBT Vật lí Lớp 11
- Bài giảng ôn luyện kiến thức môn Vật lí lớp 11
- SGK Vật lí 11 - Chân trời sáng tạo
- Chuyên đề học tập Vật lí 11 - Chân trời sáng tạo
- SBT Vật lí 11 - Cánh Diều
- SGK Vật lí 11 - Cánh Diều
- SBT Vật lí 11 - Chân trời sáng tạo
- Tổng hợp Lí thuyết Vật lí 11
- SBT Vật lí 11 - Kết nối tri thức với cuộc sống
- SGK Vật lí 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Vật lí 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Vật lí 11 - Cánh Diều
- SGK Vật lí Nâng cao Lớp 11
- SGK Vật lí Lớp 11
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- SBT Tiếng Anh Lớp 11 mới
- Đề thi, đề kiểm tra Tiếng Anh 11 mới
- SHS Tiếng Anh 11 - Explore New Worlds
- SBT Tiếng Anh 11 - Explore New Worlds
- SBT Tiếng Anh 11 - i-Learn Smart World
- SHS Tiếng Anh 11 - English Discovery
- SBT Tiếng Anh 11 - Global Success
- SHS Tiếng Anh 11 - Bright
- SBT Tiếng Anh 11 - Friends Global
- SHS Tiếng Anh 11 - i-Learn Smart World
- SHS Tiếng Anh 11 - Global Success
- SHS Tiếng Anh 11 - Friends Global
- SBT Tiếng Anh 11 - Bright
- SBT Tiếng Anh 11 - English Discovery
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 11
- Tổng hợp Lí thuyết Tiếng Anh 11
- SGK Tiếng Anh Lớp 11 mới
- SGK Tiếng Anh Lớp 11
![ảnh môn học Sinh học]() Sinh học
Sinh học
- SBT Sinh Lớp 11
- SGK Sinh học 11 - Cánh Diều
- SBT Sinh học 11 - Cánh Diều
- SBT Sinh học 11 - Kết nối tri thức với cuộc sống
- SBT Sinh học 11 - Chân trời sáng tạo
- Chuyên đề học tập Sinh học 11 - Cánh Diều
- Chuyên đề học tập Sinh học 11 - Chân trời sáng tạo
- Chuyên đề học tập Sinh học 11 - Kết nối tri thức với cuộc sống
- Tổng hợp Lí thuyết Sinh học 11
- SGK Sinh học 11 - Kết nối tri thức với cuộc sống
- SGK Sinh học 11 - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Sinh học lớp 11
- SGK Sinh Nâng cao Lớp 11
- SGK Sinh Lớp 11
![ảnh môn học Địa lí]() Địa lí
Địa lí
- SGK Địa lí Lớp 11
- SGK Địa lí 11 - Chân trời sáng tạo
- SBT Địa lí 11 - Chân trời sáng tạo
- Chuyên đề học tập Địa lí 11 - Chân trời sáng tạo
- Tổng hợp Lí thuyết Địa lí 11
- SGK Địa lí 11 - Cánh Diều
- SBT Địa lí 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Địa lí 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Địa lí 11 - Cánh Diều
- SBT Địa lí 11 - Cánh Diều
- SGK Địa lí 11 - Kết nối tri thức với cuộc sống
- Bài giảng ôn luyện kiến thức môn Địa lí lớp 11
- SBT Địa lí Lớp 11
- Tập bản đồ Địa lí Lớp 11
![ảnh môn học Công nghệ]() Công nghệ
Công nghệ
- SGK Công nghệ Lớp 11
- SGK Công nghệ 11 - Phần Cơ khí - Cánh Diều
- SGK Công nghệ 11 - Phần Cơ khí - Chân trời sáng tạo
- SGK Công nghệ 11 - Phần Chăn nuôi - Cánh Diều
- SGK Công nghệ 11 - Phần Cơ khí - Kết nối tri thức với cuộc sống
- SGK Công nghệ 11 - Phần Chăn nuôi - Kết nối tri thức với cuộc sống
- SGK Công nghệ 11 - Phần Chăn nuôi - Chân trời sáng tạo
![ảnh môn học Hóa học]() Hóa học
Hóa học
- SGK Hóa học Nâng cao Lớp 11
- Bài giảng ôn luyện kiến thức môn Hóa học lớp 11
- SBT Hóa học 11 - Kết nối tri thức với cuộc sống
- SBT Hóa học 11 - Cánh Diều
- Chuyên đề học tập Hóa học 11 - Cánh Diều
- SGK Hóa học 11 - Kết nối tri thức với cuộc sống
- SGK Hóa học 11 - Cánh Diều
- Tổng hợp Lí thuyết Hóa học 11
- SGK Hóa học 11 - Chân trời sáng tạo
- Chuyên đề học tập Hóa học 11 - Kết nối tri thức với cuộc sống
- SBT Hóa học 11 - Chân trời sáng tạo
- Chuyên đề học tập Hóa học 11 - Chân trời sáng tạo
- SGK Hóa Lớp 11
- SBT Hóa Lớp 11
![ảnh môn học Ngữ văn]() Ngữ văn
Ngữ văn
- Soạn văn chi tiết Lớp 11
- SBT Ngữ văn 11 - Chân trời sáng tạo
- Chuyên đề học tập Ngữ văn 11 - Chân trời sáng tạo
- SBT Ngữ văn 11 - Cánh Diều
- Tuyển tập những bài văn hay Ngữ văn 11 - Chân trời sáng tạo
- SGK Ngữ văn 11 - Cánh Diều
- Chuyên đề học tập Ngữ văn 11 - Kết nối tri thức với cuộc sống
- SGK Ngữ văn 11 - Kết nối tri thức với cuộc sống
- Tuyển tập những bài văn hay Ngữ văn 11 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Ngữ Văn lớp 11
- SBT Ngữ văn 11 - Kết nối tri thức với cuộc sống
- SGK Ngữ văn 11 - Chân trời sáng tạo
- Chuyên đề học tập Ngữ văn 11 - Cánh Diều
- Tuyển tập những bài văn hay Ngữ văn 11 - Kết nối tri thức với cuộc sống
- Soạn văn siêu ngắn Lớp 11
- Tác giả - Tác phẩm Lớp 11
- Văn mẫu Lớp 11
![ảnh môn học Toán học]() Toán học
Toán học
- SBT Toán Nâng cao Lớp 11
- Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Chuyên đề học tập Toán 11 - Kết nối tri thức với cuộc sống
- SGK Toán 11 - Kết nối tri thức với cuộc sống
- SBT Toán 11 - Chân trời sáng tạo
- Chuyên đề học tập Toán 11 - Cánh Diều
- SBT Toán 11 - Cánh Diều
- SBT Toán 11 - Kết nối tri thức với cuộc sống
- SGK Toán 11 - Chân trời sáng tạo
- SGK Toán 11 - Cánh Diều
- Tổng hợp Lí thuyết Toán 11
- Bài giảng ôn luyện kiến thức môn Toán lớp 11
- SBT Toán Lớp 11
- SGK Toán Nâng cao Lớp 11
- SGK Toán Lớp 11
![ảnh môn học Lịch sử]() Lịch sử
Lịch sử
- SGK Lịch sử Lớp 11
- SGK Lịch sử 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Lịch sử 11 - Cánh Diều
- SBT Lịch sử 11 - Cánh Diều
- SBT Lịch sử 11 - Kết nối tri thức với cuộc sống
- SGK Lịch sử 11 - Chân trời sáng tạo
- Chuyên đề học tập Lịch sử 11 - Chân trời sáng tạo
- SGK Lịch sử 11 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Lịch sử lớp 11
- SBT Lịch sử 11 - Chân trời sáng tạo
- Tổng hợp Lí thuyết Lịch sử 11
- Chuyên đề học tập Lịch sử 11 - Kết nối tri thức với cuộc sống
- SBT Lịch sử Lớp 11
- Tập bản đồ Lịch sử Lớp 11
![ảnh môn học Giáo dục kinh tế và pháp luật]() Giáo dục kinh tế và pháp luật
Giáo dục kinh tế và pháp luật
- SGK Giáo dục Kinh tế và Pháp luật 11 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Giáo dục kinh tế và pháp luật lớp 11
- SBT Giáo dục Kinh tế và Pháp luật 11 - Chân trời sáng tạo
- Chuyên đề học tập Giáo dục Kinh tế và Pháp luật 11 - Cánh Diều
- SGK Giáo dục Kinh tế và Pháp luật 11 - Kết nối tri thức với cuộc sống
- Chuyên đề học tập Giáo dục Kinh tế và Pháp luật 11 - Chân trời sáng tạo
- Chuyên đề học tập Giáo dục Kinh tế và Pháp luật 11 - Kết nối tri thức với cuộc sống
- SGK Giáo dục Kinh tế và Pháp luật 11 - Chân trời sáng tạo
- SBT Giáo dục Kinh tế và Pháp luật 11 - Kết nối tri thức với cuộc sống
- Tổng hợp Lí thuyết Giáo dục Kinh tế và Pháp luật 11
- SBT Giáo dục Kinh tế và Pháp luật 11 - Cánh Diều
![ảnh môn học Giáo dục thể chất]() Giáo dục thể chất
Giáo dục thể chất
- SGK Giáo dục thể chất - Đá cầu - Cánh Diều
- SGK Giáo dục thể chất - Kiến thức chung - Cánh Diều
- SGK Giáo dục thể chất - Bóng chuyền - Kết nối tri thức với cuộc sống
- SGK Giáo dục thể chất - Bóng đá - Chân trời sáng tạo
- SGK Giáo dục thể chất - Bóng rổ - Kết nối tri thức với cuộc sống
- SGK Giáo dục thể chất - Bóng đá - Cánh Diều
- SGK Giáo dục thể chất - Cầu lông - Chân trời sáng tạo
- SGK Giáo dục thể chất - Bóng chuyền - Chân trời sáng tạo
- SGK Giáo dục thể chất - Bóng đá - Kết nối tri thức với cuộc sống
- SGK Giáo dục thể chất - Cầu lông - Kết nối tri thức với cuộc sống
- SGK Giáo dục thể chất - Bóng chuyền - Cánh Diều
- SGK Giáo dục thể chất - Bóng rổ - Cánh Diều
- SGK Giáo dục thể chất - Cầu lông - Cánh Diều
- SGK Giáo dục thể chất - Bóng rổ - Chân trời sáng tạo
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- Lý thuyết Tiếng Anh Lớp 10
- Đề thi, đề kiểm tra Tiếng Anh - Bright
- Đề thi, đề kiểm tra Tiếng Anh - iLearn Smart World
- Đề thi, đề kiểm tra Tiếng Anh - Global Success
- Đề thi, đề kiểm tra Tiếng Anh - English Discovery
- Đề thi, đề kiểm tra Tiếng Anh - Friends Global
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 10
- SBT Bright Lớp 10
- SBT English Discovery Lớp 10
- SBT Friends Global Lớp 10
- SBT Global Success Lớp 10
- SBT iLearn Smart World Lớp 10
- Tiếng Anh - Bright Lớp 10
- Tiếng Anh - English Discovery Lớp 10
- Tiếng Anh - Explore New Worlds Lớp 10
- Tiếng Anh - Friends Global Lớp 10
- Tiếng Anh - Global Success Lớp 10
- Tiếng Anh - iLearn Smart World Lớp 10
![ảnh môn học Lịch sử]() Lịch sử
Lịch sử
- Chuyên đề học tập Lịch sử - Kết nối tri thức Lớp 10
- Đề thi, kiểm tra Lịch sử lớp 10
- SBT Lịch sử - Cánh diều 10
- Bài giảng ôn luyện kiến thức môn Lịch sử lớp 10
- SBT Lịch sử 10 - Chân trời sáng tạo Lớp 10
- SBT Lịch sử - Kết nối tri thức Lớp 10
- SGK Lịch sử - Cánh Diều Lớp 10
- SGK Lịch sử - Chân trời sáng tạo Lớp 10
- SGK Lịch sử - Kết nối tri thức Lớp 10
![ảnh môn học Toán học]() Toán học
Toán học
- Chuyên đề học tập Toán - Cánh diều Lớp 10
- Đề thi, đề kiểm tra Toán lớp 10 - Kết nối tri thức
- Đề thi, đề kiểm tra Toán lớp 10 - Chân trời sáng tạo
- Đề thi, đề kiểm tra Toán lớp 10 - Cánh diều
- Bài giảng ôn luyện kiến thức môn Toán lớp 10
- Chuyên đề học tập Toán - Chân trời sáng tạo Lớp 10
- Chuyên đề học tập Toán - Kết nối tri thức Lớp 10
- Lý thuyết Toán Lớp 10
- SBT Toán - Cánh Diều Lớp 10
- SBT Toán - Chân trời sáng tạo Lớp 10
- SBT Toán - Kết nối tri thức Lớp 10
- SGK Toán - Cánh diều Lớp 10
- SGK Toán - Chân trời sáng tạo Lớp 10
- SGK Toán - Kết nối tri thức Lớp 10
![ảnh môn học Ngữ văn]() Ngữ văn
Ngữ văn
- Chuyên đề học tập Văn - Cánh diều Lớp 10
- Đề thi, đề kiểm tra Ngữ văn - Kết nối tri thức lớp 10
- Đề thi, đề kiểm tra Ngữ văn - Cánh diều lớp 10
- Văn mẫu - Cánh diều Lớp 10
- Văn mẫu - Kết nối tri thức
- Đề thi, đề kiểm tra Ngữ văn - Chân trời sáng tạo lớp 10
- Văn mẫu - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Ngữ Văn lớp 10
- Chuyên đề học tập Văn - Chân trời sáng tạo Lớp 10
- Chuyên đề học tập Văn - Kết nối tri thức Lớp 10
- Lý thuyết Văn Lớp 10
- SBT Văn - Cánh diều Lớp 10
- SBT Văn - Chân trời sáng tạo Lớp 10
- SBT Văn - Kết nối tri thức Lớp 10
- Soạn văn - Cánh Diều - chi tiết Lớp 10
- Soạn văn - Cánh Diều - siêu ngắn Lớp 10
- Soạn văn - Chân trời sáng tạo - chi tiết Lớp 10
- Soạn văn - Chân trời sáng tạo - siêu ngắn Lớp 10
- Soạn văn - Kết nối tri thức - chi tiết Lớp 10
- Soạn văn - Kết nối tri thức - siêu ngắn Lớp 10
- Tác giả tác phẩm Lớp 10
![ảnh môn học Sinh học]() Sinh học
Sinh học
- Chuyên đề học tập Sinh - Chân trời sáng tạo Lớp 10
- Đề thi, kiểm tra Sinh - Kết nối tri thức
- Đề thi, đề kiểm tra Sinh học 10
- Đề thi, kiểm tra Sinh - Cánh diều
- Đề thi, kiểm tra Sinh - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Sinh học lớp 10
- Chuyên đề học tập Sinh - Kết nối tri thức Lớp 10
- Lý thuyết Sinh Lớp 10
- SBT Sinh - Cánh diều Lớp 10
- SBT Sinh - Chân trời sáng tạo Lớp 10
- SBT Sinh - Kết nối tri thức Lớp 10
- SGK Sinh - Cánh diều Lớp 10
- SGK Sinh - Chân trời sáng tạo Lớp 10
- SGK Sinh - Kết nối tri thức Lớp 10
![ảnh môn học Hóa học]() Hóa học
Hóa học
- Chuyên đề học tập Hóa - Chân trời sáng tạo Lớp 10
- Đề thi, đề kiểm tra Hóa lớp 10 – Cánh diều
- Đề thi, đề kiểm tra Hóa lớp 10 – Kết nối tri thức
- Đề thi, đề kiểm tra Hóa lớp 10 – Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Hóa học lớp 10
- Chuyên đề học tập Hóa - Kết nối tri thức Lớp 10
- SBT Hóa 10 - Cánh diều Lớp 10
- SBT Hóa - Chân trời sáng tạo Lớp 10
- SBT Hóa - Kết nối tri thức Lớp 10
- SGK Hóa - Cánh diều Lớp 10
- SGK Hóa - Chân trời sáng tạo Lớp 10
- SGK Hóa - Kết nối tri thức Lớp 10
- Chuyên đề học tập Hóa - Cánh diều Lớp 10
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- SGK Tiếng Anh Lớp 8 mới
- Đề thi, đề kiểm tra Tiếng Anh 8 mới
- SHS Tiếng Anh 8 - Global Success
- SHS Tiếng Anh 8 - Explore English
- SBT Tiếng Anh 8 - Global Success
- SBT Tiếng Anh 8 - THiNK
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 8
- SBT Tiếng Anh 8 - Macmillan Motivate
- SBT Tiếng Anh 8 - Right on!
- SBT Tiếng Anh 8 - Explore English
- SBT Tiếng Anh 8 - English Discovery
- SBTTiếng Anh 8 - i-Learn Smart World
- SBT Tiếng Anh 8 - Friends Plus
- SGK Tiếng Anh Lớp 8
- SBT Tiếng Anh Lớp 8 mới
- Vở bài tập Tiếng Anh Lớp 8
![ảnh môn học GDCD]() GDCD
GDCD
- Bài tập tình huống GDCD Lớp 8
- SBT Giáo dục công dân 8 - Kết nối tri thức với cuộc sống
- SGK Giáo dục công dân 8 - Chân trời sáng tạo
- SGK Giáo dục công dân 8 - Kết nối tri thức với cuộc sống
- SBT Giáo dục công dân 8 - Chân trời sáng tạo
- Tổng hợp Lí thuyết Giáo dục công dân 8
- SGK Giáo dục công dân 8 - Cánh Diều
- SBT Giáo dục công dân 8 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Giáo dục công dân lớp 8
- SGK GDCD Lớp 8
![ảnh môn học Ngữ văn]() Ngữ văn
Ngữ văn
- Soạn văn siêu ngắn Lớp 8
- Tuyển tập những bài văn hay Ngữ văn 8 - Chân trời sáng tạo
- SBT Ngữ văn 8 - Chân trời sáng tạo
- Tuyển tập những bài văn hay Ngữ văn 8 - Kết nối tri thức với cuộc sống
- SBT Ngữ văn 8 - Kết nối tri thức với cuộc sống
- SGK Ngữ văn 8 - Cánh Diều
- VBT Ngữ văn 8 - Kết nối tri thức với cuộc sống
- Bài giảng ôn luyện kiến thức môn Ngữ Văn lớp 8
- Tổng hợp Lí thuyết Ngữ văn 8
- SGK Ngữ văn 8 - Kết nối tri thức với cuộc sống
- Tuyển tập những bài văn hay Ngữ văn 8 - Cánh Diều
- SGK Ngữ văn 8 - Chân trời sáng tạo
- SBT Ngữ văn 8 - Cánh Diều
- Soạn văn chi tiết Lớp 8
- Tác giả - Tác phẩm văn Lớp 8
- Văn mẫu Lớp 8
- Vở bài tập Ngữ văn Lớp 8
![ảnh môn học Toán học]() Toán học
Toán học
- SGK Toán Lớp 8
- SGK Toán 8 - Chân trời sáng tạo
- SBT Toán 8 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Toán lớp 8
- SGK Toán 8 - Cánh Diều
- VBT Toán 8 - Kết nối tri thức với cuộc sống
- SBT Toán 8 - Kết nối tri thức với cuộc sống
- SGK Toán 8 - Kết nối tri thức với cuộc sống
- Tổng hợp Lí thuyết Toán 8
- SBT Toán Lớp 8
- Giải bài tập Toán Lớp 8
- Tài liệu Dạy - học Toán Lớp 8
- Đề thi, đề kiểm tra Toán Lớp 8
![ảnh môn học Lịch sử và Địa lí]() Lịch sử và Địa lí
Lịch sử và Địa lí
- Bài giảng ôn luyện kiến thức môn Địa lí lớp 8
- SGK Lịch sử và Địa lí 8 - Chân trời sáng tạo
- SBT Lịch sử và Địa lí 8 - Chân trời sáng tạo
- SBT Lịch sử và Địa lí 8 - Kết nối tri thức với cuộc sống
- SGK Lịch sử và Địa lí 8 - Cánh Diều
- SBT Lịch sử và Địa lí 8 - Cánh Diều
- SGK Lịch sử và Địa lí 8 - Kết nối tri thức với cuộc sống 1
- Tổng hợp Lí thuyết Lịch sử và Địa lí 8
- Bài giảng ôn luyện kiến thức môn Lịch sử lớp 8
![ảnh môn học Khoa học tự nhiên]() Khoa học tự nhiên
Khoa học tự nhiên
- SGK Khoa học tự nhiên 8 - Kết nối tri thức với cuộc sống
- SGK Khoa học tự nhiên 8 - Cánh Diều
- SBT Khoa học tự nhiên 8 - Chân trời sáng tạo
- SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- SBT Khoa học tự nhiên 8 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Khoa học tự nhiên lớp 8
- Tổng hợp Lí thuyết Khoa học tự nhiên 8
- SBT Khoa học tự nhiên 8 - Kết nối tri thức với cuộc sống
![ảnh môn học Khoa học tự nhiên]() Khoa học tự nhiên
Khoa học tự nhiên
- Lý thuyết Khoa học tự nhiên Lớp 7
- Đề thi, đề kiểm tra KHTN - Kết nối tri thức
- Đề thi, đề kiểm tra KHTN - Chân trời sáng tạo
- Đề thi, đề kiểm tra KHTN - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Khoa học tự nhiên lớp 7
- SBT KHTN - Cánh diều Lớp 7
- SBT KHTN - Chân trời sáng tạo Lớp 7
- SBT KHTN - Kết nối tri thức Lớp 7
- SGK Khoa học tự nhiên - Cánh diều Lớp 7
- SGK Khoa học tự nhiên - Chân trời sáng tạo Lớp 7
- SGK Khoa học tự nhiên - Kết nối tri thức Lớp 7
- Vở thực hành Khoa học tự nhiên Lớp 7
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- Lý thuyết Tiếng Anh Lớp 7
- Đề thi, đề kiểm tra Tiếng Anh - Right on!
- Đề thi, đề kiểm tra Tiếng Anh - English Discovery
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 7
- SBT English Discovery Lớp 7
- SBT Friends Plus Lớp 7
- SBT Global Success Lớp 7
- SBT iLearn Smart World Lớp 7
- SBT Right on! Lớp 7
- Tiếng Anh - English Discovery Lớp 7
- Tiếng Anh - Friends Plus Lớp 7
- Tiếng Anh - iLearn Smart World Lớp 7
- Tiếng Anh - Right on! Lớp 7
- Tiếng Anh - Global Success Lớp 7
- Đề thi, đề kiểm tra Tiếng Anh - Friends Plus
- Đề thi, đề kiểm tra Tiếng Anh - Global Success
- Đề thi, đề kiểm tra Tiếng Anh - iLearn Smart World
![ảnh môn học Lịch sử và Địa lí]() Lịch sử và Địa lí
Lịch sử và Địa lí
- SBT Lịch sử và Địa lí - Chân trời sáng tạo Lớp 7
- SBT Lịch sử và Địa lí - Cánh diều lớp 7
- Bài giảng ôn luyện kiến thức môn Địa lí lớp 7
- Bài giảng ôn luyện kiến thức môn Lịch sử lớp 7
- SBT Lịch sử và Địa lí - Kết nối tri thức Lớp 7
- SGK Lịch sử và Địa lí - Cánh Diều Lớp 7
- SGK Lịch sử và Địa lí - Chân trời sáng tạo Lớp 7
- SGK Lịch sử và Địa lí - Kết nối tri thức Lớp 7
![ảnh môn học Ngữ văn]() Ngữ văn
Ngữ văn
- Đề thi, đề kiểm tra Văn - Cánh diều Lớp 7
- Bài tập trắc nghiệm Văn 7 - Kết nối tri thức
- Bài tập trắc nghiệm Văn 7 - Cánh diều
- Bài tập trắc nghiệm Văn 7 - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Ngữ Văn lớp 7
- Đề thi, đề kiểm tra Văn - Chân trời sáng tạo Lớp 7
- Đề thi, đề kiểm tra Văn - Kết nối tri thức Lớp 7
- Lý thuyết Văn Lớp 7
- SBT Văn - Cánh diều Lớp 7
- SBT Văn - Chân trời sáng tạo Lớp 7
- SBT Văn - Kết nối tri thức Lớp 7
- Soạn văn chi tiết - Cánh diều Lớp 7
- Soạn văn siêu ngắn - Cánh diều Lớp 7
- Soạn văn chi tiết - CTST Lớp 7
- Soạn văn siêu ngắn - CTST Lớp 7
- Soạn văn chi tiết - KNTT Lớp 7
- Soạn văn siêu ngắn - KNTT Lớp 7
- Tác giả - Tác phẩm văn Lớp 7
- Văn mẫu - Cánh Diều Lớp 7
- Văn mẫu - Chân trời sáng tạo Lớp 7
- Văn mẫu - Kết nối tri thức Lớp 7
- Vở thực hành văn Lớp 7
![ảnh môn học Toán học]() Toán học
Toán học
- Đề thi, đề kiểm tra Toán - Chân trời sáng tạo Lớp 7
- Bài tập trắc nghiệm Toán - Kết nối tri thức
- Đề thi, đề kiểm tra Toán - Cánh diều Lớp 7
- Bài tập trắc nghiệm Toán - Cánh diều
- Đề thi, đề kiểm tra Toán - Kết nối tri thức Lớp 7
- Bài tập trắc nghiệm Toán - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Toán lớp 7
- Lý thuyết Toán Lớp 7
- SBT Toán - Cánh diều Lớp 7
- SBT Toán - Chân trời sáng tạo Lớp 7
- SBT Toán - Kết nối tri thức Lớp 7
- SGK Toán - Cánh diều Lớp 7
- SGK Toán - Chân trời sáng tạo Lớp 7
- SGK Toán - Kết nối tri thức Lớp 7
- Tài liệu Dạy - học Toán Lớp 7
- Vở thực hành Toán Lớp 7
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- Ôn tập hè Tiếng Anh lớp 6
- Bài tập trắc nghiệm Tiếng Anh - iLearn Smart World
- Bài tập trắc nghiệm Tiếng Anh 6 - English Discovery
- Bài tập trắc nghiệm Tiếng Anh - Friends Plus
- Bài tập trắc nghiệm Tiếng Anh - Global Success
- Bài tập trắc nghiệm Tiếng Anh - Right on!
- SBT Global Success Lớp 6
- SBT English Discovery Lớp 6
- SBT Friends Plus Lớp 6
- SBT iLearn Smart World Lớp 6
- SBT Right on! Lớp 6
- Tiếng Anh - Explore English Lớp 6
- Tiếng Anh - Friends plus Lớp 6
- Tiếng Anh - English Discovery Lớp 6
- Global Success (Pearson) Lớp 6
- Tiếng Anh - iLearn Smart World Lớp 6
- Tiếng Anh - Right on Lớp 6
- Đề thi, đề kiểm tra Tiếng Anh - English Discovery
- Đề thi, đề kiểm tra Tiếng Anh - Friends Plus
- Đề thi, đề kiểm tra Tiếng Anh - iLearn Smart World
- Đề thi, đề kiểm tra Tiếng Anh - Global Success
- Đề thi, đề kiểm tra Tiếng Anh - Right on!
![ảnh môn học Khoa học tự nhiên]() Khoa học tự nhiên
Khoa học tự nhiên
- SGK KHTN - Cánh Diều Lớp 6
- Đề thi, đề kiểm tra KHTN - Kết nối tri thức
- Đề thi, đề kiểm tra KHTN - Chân trời sáng tạo
- Đề thi, đề kiểm tra KHTN - Cánh diều
- Bài giảng ôn luyện kiến thức môn Khoa học tự nhiên lớp 6
- SGK KHTN - Chân trời sáng tạo Lớp 6
- SGK KHTN - Kết nối tri thức Lớp 6
- SBT KHTN - Cánh Diều Lớp 6
- SBT KHTN - Chân trời sáng tạo Lớp 6
- SBT KHTN - Kết nối tri thức Lớp 6
- Vở thực hành Khoa học tự nhiên Lớp 6
![ảnh môn học HĐ trải nghiệm, hướng nghiệp]() HĐ trải nghiệm, hướng nghiệp
HĐ trải nghiệm, hướng nghiệp
- SGK Trải nghiệm, hướng nghiệp - Cánh diều Lớp 6
- SGK Trải nghiệm, hướng nghiệp - Chân trời sáng tạo Lớp 6
- SGK Trải nghiệm, hướng nghiệp - Kết nối tri thức Lớp 6
- SBT Trải nghiệm, hướng nghiệp - Chân trời sáng tạo Lớp 6
- SBT Trải nghiệm, hướng nghiệp - Kết nối tri thức Lớp 6
- Thực hành Trải nghiệm, hướng nghiệp - Cánh diều Lớp 6
![ảnh môn học Lịch sử và Địa lí]() Lịch sử và Địa lí
Lịch sử và Địa lí
- SGK Lịch sử và Địa lí - Cánh Diều Lớp 6
- Đề thi, kiểm tra Lịch sử và Địa lí - Kết nối tri thức
- Đề thi, kiểm tra Lịch sử và Địa lí - Cánh Diều
- Đề thi, kiểm tra Lịch sử và Địa lí - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Địa lí lớp 6
- Bài giảng ôn luyện kiến thức môn Lịch sử lớp 6
- SGK Lịch sử và Địa lí - CTST Lớp 6
- SGK Lịch sử và Địa lí - KNTT Lớp 6
- SBT Lịch sử và Địa lí - KNTT Lớp 6
- SBT Lịch sử và Địa lí - Cánh diều Lớp 6
- SBT Lịch sử và Địa lí - CTST Lớp 6
![ảnh môn học Ngữ văn]() Ngữ văn
Ngữ văn
- Đề thi, đề kiểm tra Văn - Cánh diều Lớp 6
- Bài tập trắc nghiệm Văn - Kết nối tri thức
- Bài tập trắc nghiệm Văn - Chân trời sáng tạo
- Đề thi, đề kiểm tra Văn - Kết nối tri thức
- Bài tập trắc nghiệm Văn - Cánh diều
- Bài giảng ôn luyện kiến thức môn Ngữ Văn lớp 6
- Đề thi, đề kiểm tra Văn - Chân trời sáng tạo Lớp 6
- Đề thi, đề kiểm tra Văn - Kết nối tri thức Lớp 6
- SBT Văn - Chân trời sáng tạo Lớp 6
- Ôn tập hè Văn Lớp 6
- SBT Văn - Cánh diều Lớp 6
- SBT Văn - Kết nối tri thức Lớp 6
- Soạn văn chi tiết - Cánh diều Lớp 6
- Soạn văn siêu ngắn - Cánh diều Lớp 6
- Soạn văn chi tiết - CTST Lớp 6
- Soạn văn siêu ngắn - CTST Lớp 6
- Soạn văn chi tiết - KNTT Lớp 6
- Soạn văn siêu ngắn - KNTT Lớp 6
- Tác giả - Tác phẩm văn Lớp 6
- Văn mẫu - Cánh Diều Lớp 6
- Văn mẫu - Kết nối tri thức Lớp 6
- Văn mẫu - Chân trời sáng tạo Lớp 6
- Vở thực hành văn Lớp 6
![ảnh môn học Toán học]() Toán học
Toán học
- Ôn tập hè Toán Lớp 6
- Bài tập trắc nghiệm Toán - Cánh diều
- Bài tập trắc nghiệm Toán - Kết nối tri thức
- Bài tập trắc nghiệm Toán 6 - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Toán lớp 6
- SBT Toán - Cánh diều Lớp 6
- SBT Toán - Kết nối tri thức Lớp 6
- SBT Toán - Chân trời sáng tạo Lớp 6
- Tài liệu Dạy - học Toán Lớp 6
- SGK Toán - Cánh diều Lớp 6
- SGK Toán - Chân trời sáng tạo Lớp 6
- SGK Toán - Kết nối tri thức Lớp 6
- Đề thi, đề kiểm tra Toán - Cánh diều
- Đề thi, đề kiểm tra Toán - Chân trời sáng tạo
- Đề thi, đề kiểm tra Toán - Kết nối tri thức
- Vở thực hành Toán Lớp 6
![ảnh môn học Toán học]() Toán học
Toán học
- SGK Toán Lớp 5
- Bài tập trắc nghiệm Toán 5
- Công thức Toán lớp 5
- Toán nâng cao lớp 5
- Bài giảng ôn luyện kiến thức môn Toán lớp 5
- Kết nối tri thức
- VNEN Toán Lớp 5
- Vở bài tập Toán Lớp 5
- Bài tập cuối tuần Toán Lớp 5
- Cùng em học toán Lớp 5
- Đề thi, đề kiểm tra Toán Lớp 5
- Bài tập phát triển năng lực Toán Lớp 5
![ảnh môn học Lịch sử và Địa lí]() Lịch sử và Địa lí
Lịch sử và Địa lí
- SGK Lịch sử và Địa lí Lớp 4
- SGK Lịch sử và Địa lí 4 - Cánh Diều
- VBT Lịch sử và Địa lí 4 - Chân trời sáng tạo
- SGK Lịch sử và Địa lí 4 - Kết nối tri thức với cuộc sống
- VBT Lịch sử và Địa lí 4 - Cánh Diều
- SGK Lịch sử và Địa lí 4 - Chân trời sáng tạo
- VBT Lịch sử và Địa lí 4 - Kết nối tri thức với cuộc sống
- Vở bài tập Lịch sử Lớp 4
- Vở bài tập Địa lí Lớp 4
![ảnh môn học Toán học]() Toán học
Toán học
- SGK Toán Lớp 4
- SGK Toán 4 - Kết nối tri thức với cuộc sống
- STK - Cùng em phát triển năng lực Toán 4
- Bài giảng ôn luyện kiến thức môn Toán lớp 4
- SGK Toán 4 - Chân trời sáng tạo
- SGK Toán 4 - Cánh Diều
- VBT Toán 4 - Chân trời sáng tạo
- VBT Toán 4 - Kết nối tri thức với cuộc sống
- VBT Toán 4 - Cánh Diều
- VNEN Toán Lớp 4
- Vở bài tập Toán Lớp 4
- Bài tập cuối tuần Toán Lớp 4
- Cùng em học toán Lớp 4
- Ôn tập hè Toán Lớp 4
- Đề thi, đề kiểm tra Toán Lớp 4
- Bài tập phát triển năng lực Toán Lớp 4
![ảnh môn học Tiếng việt]() Tiếng việt
Tiếng việt
- SGK Tiếng Việt Lớp 4
- VBT Tiếng Việt 4 - Cánh Diều
- SGK Tiếng Việt 4 - Chân trời sáng tạo
- VBT Tiếng Việt 4 - Chân trời sáng tạo
- SGK Tiếng Việt 4 - Kết nối tri thức với cuộc sống
- VBT Tiếng Việt 4 - Kết nối tri thức với cuộc sống
- SGK Tiếng Việt 4 - Cánh Diều
- Bài giảng ôn luyện kiến thức môn Tiếng Việt lớp 4
- Cùng em học Tiếng Việt Lớp 4
- VNEN Tiếng Việt Lớp 4
- Vở bài tập Tiếng Việt Lớp 4
- Văn mẫu Lớp 4
- Đề thi, đề kiểm tra Tiếng Việt Lớp 4
- Ôn tập hè Tiếng Việt Lớp 4
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- SGK Tiếng Anh Lớp 4 Mới
- Đề thi, đề kiểm tra Tiếng Anh lớp 4
- SHS Tiếng Anh 4 - Family and Friends
- SHS Tiếng Anh 4 - i-Learn Smart Start
- SBT Tiếng Anh 4 - Explore Our World
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 4
- SBT Tiếng Anh 4 - i-Learn Smart Start
- SHS Tiếng Anh 4 - Phonics-Smart
- SBT Tiếng Anh 4 - Global Success
- SHS Tiếng Anh 4 - Explore Our World
- SBT Tiếng Anh 4 - Phonics-Smart
- SHS Tiếng Anh 4 - Global Success
- SBT Tiếng Anh 4 - Family and Friends
- SBT Tiếng Anh Lớp 4
- Ôn tập hè Tiếng Anh Lớp 4
![ảnh môn học Toán học]() Toán học
Toán học
- Bài tập cuối tuần môn Toán Lớp 3
- Bài tập trắc nghiệm Toán - Kết nối tri thức
- Đề thi, đề kiểm tra Toán - Chân trời sáng tạo
- Bài tập trắc nghiệm Toán - Chân trời sáng tạo
- Bài tập trắc nghiệm Toán - Cánh diều
- Đề thi, đề kiểm tra Toán - Kết nối tri thức
- Đề thi, đề kiểm tra Toán - Cánh diều
- Bài giảng ôn luyện kiến thức môn Toán lớp 3
- Cùng em học Toán Lớp 3
- SGK Toán - Cánh diều Lớp 3
- SGK Toán - Chân trời sáng tạo Lớp 3
- SGK Toán - Kết nối tri thức Lớp 3
- VBT Toán - Kết nối tri thức Lớp 3
![ảnh môn học Tiếng việt]() Tiếng việt
Tiếng việt
- Cùng em học Tiếng Việt Lớp 3
- VBT Tiếng Việt - Cánh diều Lớp 3
- Đề thi, đề kiểm tra Tiếng Việt 3
- Bài giảng ôn luyện kiến thức môn Tiếng Việt lớp 3
- Tiếng Việt - Cánh diều Lớp 3
- Tiếng Việt - Chân trời sáng tạo Lớp 3
- Tiếng Việt - Kết nối tri thức Lớp 3
- Văn mẫu - Kết nối tri thức Lớp 3
- Văn mẫu Lớp 3
- VBT Tiếng Việt - Chân trời sáng tạo Lớp 3
- VBT Tiếng Việt - Kết nối tri thức Lớp 3
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- Bài tập trắc nghiệm Tiếng Anh - Family and Friends
- Đề thi, đề kiểm tra Tiếng Anh - Family and Friends Lớp 3
- Bài tập trắc nghiệm Tiếng Anh - iLearn Smart Start
- Bài tập trắc nghiệm Tiếng Anh - Global Success
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 3
- Đề thi, đề kiểm tra Tiếng Anh - Global Success Lớp 3
- Đề thi, đề kiểm tra Tiếng Anh - iLearn Smart Start Lớp 3
- SBT Tiếng Anh - Family and Friends Lớp 3
- SBT Tiếng Anh - iLearn Smart Start Lớp 3
- SBT Tiếng Anh - Global Success Lớp 3
- SBT Tiếng Anh - Phonics Smart Lớp 3
- Tiếng Anh 3 - Explore Our World Lớp 3
- Tiếng Anh - Family and Friends Lớp 3
- Đề thi, đề kiểm tra Tiếng Anh - Explore Our World
- Tiếng Anh - Global Success Lớp 3
- Tiếng Anh - iLearn Smart Start Lớp 3
- Đề thi, đề kiểm tra Tiếng Anh - Phonics Smart
- Tiếng Anh 3 - Phonics Smart Lớp 3
![ảnh môn học Tiếng việt]() Tiếng việt
Tiếng việt
- Tiếng Việt - Kết nối tri thức Lớp 2
- Bài giảng ôn luyện kiến thức môn Tiếng Việt lớp 2
- Tiếng Việt - Chân trời sáng tạo Lớp 2
- Tiếng Việt - Cánh Diều Lớp 2
- Văn mẫu - Kết nối tri thức Lớp 2
- Văn mẫu - Chân trời sáng tạo Lớp 2
- Văn mẫu - Cánh diều Lớp 2
- VBT Tiếng Việt - Kết nối tri thức Lớp 2
- VBT Tiếng Việt - Chân trời sáng tạo Lớp 2
- VBT Tiếng Việt - Cánh diều Lớp 2
- Cùng em học Tiếng Việt Lớp 2
![ảnh môn học Tiếng Anh]() Tiếng Anh
Tiếng Anh
- Tiếng Anh - Kết nối tri thức Lớp 2
- Đề thi, đề kiểm tra Tiếng Anh - Global Success
- Đề thi, đề kiểm tra Tiếng Anh - iLearn Smart Start
- Đề thi, đề kiểm tra Tiếng Anh - Phonics Smart
- Đề thi, đề kiểm tra Tiếng Anh - English Discovery
- Đề thi, đề kiểm tra Tiếng Anh - Family and Friends
- Bài giảng ôn luyện kiến thức môn Tiếng Anh lớp 2
- Tiếng Anh - Family and Friends Lớp 2
- Tiếng Anh - iLearn Smart Start Lớp 2
- Tiếng Anh - Phonics Smart Lớp 2
- Tiếng Anh - English Discovery Lớp 2
- Tiếng Anh - Explore Our World Lớp 2
- Family & Friends Special Grade Lớp 2
- SBT Kết nối tri thức Lớp 2
- SBT Family and Friends Lớp 2
- SBT iLearn Smart Start Lớp 2
- SBT Phonics Smart Lớp 2
- SBT English Discovery Lớp 2
- SBT Explore Our World Lớp 2
![ảnh môn học Toán học]() Toán học
Toán học
- SGK Toán - Kết nối tri thức Lớp 2
- Bài tập trắc nghiệm Toán - Kết nối tri thức
- Bài tập trắc nghiệm Toán - Cánh diều
- Đề thi, đề kiểm tra Toán - Chân trời sáng tạo
- Đề thi, đề kiểm tra Toán - Kết nối tri thức
- Đề thi, đề kiểm tra Toán - Cánh diều
- Bài tập trắc nghiệm Toán - Chân trời sáng tạo
- Bài giảng ôn luyện kiến thức môn Toán lớp 2
- SGK Toán - Chân trời sáng tạo Lớp 2
- SGK Toán - Cánh Diều Lớp 2
- VBT Toán - KNTT Lớp 2
- VBT Toán - CTST Lớp 2
- Cùng em học Toán 2
- Bài tập cuối tuần Toán Lớp 2
Bài 6 trang 223 Sách bài tập Hình học lớp 12 Nâng cao.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng đáy. Một mặt phẳng đi qua CD cất các cạnh SA, SB lần lượt tại M, N. Đặt AM = x.
LG a
Tứ giác MNCD là hình gì ? Tính diện tích tứ giác MNCD theo a, x.
Lời giải chi tiết:
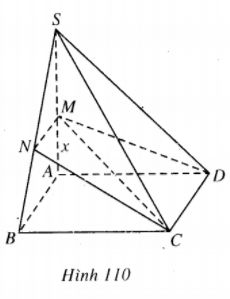
Do \(AB//CD,{\rm{ }}AB \subset \left( {SAB} \right),{\rm{ }}CD \subset \left( {MNCD} \right)\) nên hai mặt phẳng (SAB) và (MNCD) cắt nhau theo giao tuyến MN song song với AB và CD.
Mặt khác \(CD \bot \left( {SAD} \right) \Rightarrow CD \bot DM.\)
Vậy MNCD là hình thang vuông.
Vì MN//AB nên ta có \({{MN} \over {AB}} = {{SM} \over {SA}}.\)
Vây \(MN = {{AB.SM} \over {SA}} = {{aSM} \over a} = SM = a - x.\)
\({S_{MNCD}} = {1 \over 2}\left( {MN{\rm{ }} + {\rm{ }}CD} \right).DM\)
\(\eqalign{ & = {1 \over 2}\left( {a - {\rm{ }}x + a} \right)\sqrt {{a^2} + {x^2}} \cr & = {1 \over 2}\left( {2a - {\rm{ }}x} \right)\sqrt {{a^2} + {x^2}} . \cr} \)
LG b
Xác định giá trị của x để thể tích của hình chóp S.MNCD bằng \({2 \over 9}\) lần thể tích hình chóp S.ABCD.
Lời giải chi tiết:
\({S_{ABCD}} = {1 \over 3}{S_{ABCD}}.SA = {1 \over 3}{a^3}\)
\(= > {V_{S.ACD}}{\rm{ }} = {V_{S.ACB}} = {1 \over 6}{a^3}.\)
\({V_{S.MNCD}} = {V_{S.MNC}} + {V_{S.MCD}}.\)
Mặt khác
\({{{V_{S.MCN}}} \over {{V_{S.ACB}}}} = {{SM} \over {SA}}.{{SC} \over {SC}}.{{SN} \over {SB}} = {\left( {{{a - x} \over a}} \right)^2}\)
\(\Rightarrow {{{V_{S.MCN}}} \over {{V_{S.ABCD}}}} = {1 \over 2}{\left( {{{a - x} \over a}} \right)^2}.\)
\({{{V_{S.MCD}}} \over {{V_{S.ACD}}}} = {{SM} \over {SA}}.{{SC} \over {SC}}.{{SD} \over {SD}}={{SM} \over {SA} }= {{a - x} \over a} \)
\(\Rightarrow {{{V_{S.MCD}}} \over {{V_{S.ABCD}}}} = {{a - x} \over {2a}}.\)
\({{{V_{S.MNCD}}} \over {{V_{S.ABCD}}}} = {{{V_{S.MCN}} + {V_{S.MCD}}} \over {{V_{S.ABCD}}}} = {{{V_{S.MCN}}} \over {{V_{S.ABCD}}}} + {{{V_{S.MCD}}} \over {{V_{S.ABCD}}}} \)
\( = {1 \over 2}{\left( {{{a - x} \over a}} \right)^2} + {{a - x} \over {2a}}.\)
Từ đó ta có \({{{V_{S.MNCD}}} \over {{V_{S.ABCD}}}} = {2 \over 9} \Leftrightarrow {\rm{ }}9{x^2} - {\rm{ }}27ax + 14{a^2} = {\rm{ }}0\)
\(\Leftrightarrow \left[ \matrix{ x = {7 \over 3}a\text{ ( loại vì theo giả thiết x < a)}\hfill \cr x = {2 \over 3}a \hfill \cr} \right.\)
Gợi ý sách
Tải 5 đề kiểm tra 45 phút (1 tiết ) – Chương 8 – Hóa học 12
PHẦN MỘT. LỊCH SỬ THẾ GIỚI HIỆN ĐẠI TỪ NĂM 1945 ĐẾN NĂM 2000
Tải 10 đề kiểm tra 15 phút - Chương 6 – Hóa học 12
CHƯƠNG VII. HẠT NHÂN NGUYÊN TỬ
Chương 6. KIM LOẠI KIỀM, KIM LOẠI KIỀM THỔ, NHÔM



