logo home fqa
Hỏi đáp bài tập Giải bài tập SGK Cẩm nang học tập Ôn luyện
Công cụ
couple cloud tutor-icon Đăng ký học gia sư
Công thức Toán học Công thức Tiếng anh Máy tính Casio Bảng tuần hoàn hóa học Tra cứu điểm chuẩn vào 10 Tra cứu điểm chuẩn đại học
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Lớp 12
Lớp 11
Lớp 10
Lớp 9
Lớp 8
Lớp 7
Lớp 6
Lớp 5
Lớp 4
Lớp 3
Lớp 2
Lớp 1

ảnh môn học Vật lí Vật lí

ảnh môn học GDCD GDCD

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học Sinh học Sinh học

ảnh môn học Tin học Tin học

ảnh môn học Địa lí Địa lí

ảnh môn học Công nghệ Công nghệ

ảnh môn học Hóa học Hóa học

ảnh môn học Ngữ văn Ngữ văn

ảnh môn học Toán học Toán học

ảnh môn học Lịch sử Lịch sử

ảnh môn học Giáo dục kinh tế và pháp luật Giáo dục kinh tế và pháp luật

ảnh môn học Giáo dục thể chất Giáo dục thể chất

ảnh môn học Giáo dục Quốc phòng và An ninh Giáo dục Quốc phòng và An ninh

ảnh môn học HĐ trải nghiệm, hướng nghiệp HĐ trải nghiệm, hướng nghiệp

ảnh môn học Tin học Tin học

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học HĐ trải nghiệm, hướng nghiệp HĐ trải nghiệm, hướng nghiệp

ảnh môn học Lịch sử Lịch sử

ảnh môn học Toán học Toán học

ảnh môn học Ngữ văn Ngữ văn

ảnh môn học Sinh học Sinh học

ảnh môn học Địa lí Địa lí

ảnh môn học GD Quốc phòng và An ninh GD Quốc phòng và An ninh

ảnh môn học Giáo dục thể chất Giáo dục thể chất

ảnh môn học GDCD GDCD

ảnh môn học Hóa học Hóa học

ảnh môn học Công nghệ Công nghệ

ảnh môn học Vật lí Vật lí

ảnh môn học Giáo dục kinh tế và pháp luật Giáo dục kinh tế và pháp luật

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học Toán học Toán học

ảnh môn học Vật lí Vật lí

ảnh môn học Sinh học Sinh học

ảnh môn học Ngữ văn Ngữ văn

ảnh môn học Hóa học Hóa học

ảnh môn học Âm nhạc và mỹ thuật Âm nhạc và mỹ thuật

ảnh môn học Công nghệ Công nghệ

ảnh môn học Địa lí Địa lí

ảnh môn học Tin học Tin học

ảnh môn học Lịch sử Lịch sử

ảnh môn học GDCD GDCD

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học Sinh học Sinh học

ảnh môn học Tin học Tin học

ảnh môn học Lịch sử Lịch sử

ảnh môn học Âm nhạc và mỹ thuật Âm nhạc và mỹ thuật

ảnh môn học GDCD GDCD

ảnh môn học Công nghệ Công nghệ

ảnh môn học Ngữ văn Ngữ văn

ảnh môn học Hóa học Hóa học

ảnh môn học Vật lí Vật lí

ảnh môn học Địa lí Địa lí

ảnh môn học Toán học Toán học

ảnh môn học Lịch sử và Địa lí Lịch sử và Địa lí

ảnh môn học Khoa học tự nhiên Khoa học tự nhiên

ảnh môn học HĐ trải nghiệm, hướng nghiệp HĐ trải nghiệm, hướng nghiệp

ảnh môn học Giáo dục thể chất Giáo dục thể chất

ảnh môn học Âm nhạc Âm nhạc

ảnh môn học GDCD GDCD

ảnh môn học HĐ trải nghiệm, hướng nghiệp HĐ trải nghiệm, hướng nghiệp

ảnh môn học Khoa học tự nhiên Khoa học tự nhiên

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học Công nghệ Công nghệ

ảnh môn học Lịch sử và Địa lí Lịch sử và Địa lí

ảnh môn học Âm nhạc Âm nhạc

ảnh môn học Tin học Tin học

ảnh môn học Ngữ văn Ngữ văn

ảnh môn học Toán học Toán học

ảnh môn học Mỹ thuật Mỹ thuật

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học Khoa học tự nhiên Khoa học tự nhiên

ảnh môn học HĐ trải nghiệm, hướng nghiệp HĐ trải nghiệm, hướng nghiệp

ảnh môn học Tin học Tin học

ảnh môn học Âm nhạc Âm nhạc

ảnh môn học GDCD GDCD

ảnh môn học Lịch sử và Địa lí Lịch sử và Địa lí

ảnh môn học Công nghệ Công nghệ

ảnh môn học Ngữ văn Ngữ văn

ảnh môn học Toán học Toán học

ảnh môn học Tin học Tin học

ảnh môn học Lịch sử và Địa lí Lịch sử và Địa lí

ảnh môn học Tiếng việt Tiếng việt

ảnh môn học Đạo đức Đạo đức

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học Khoa học Khoa học

ảnh môn học Toán học Toán học

ảnh môn học Tin học Tin học

ảnh môn học Khoa học Khoa học

ảnh môn học Lịch sử và Địa lí Lịch sử và Địa lí

ảnh môn học Đạo đức Đạo đức

ảnh môn học Toán học Toán học

ảnh môn học Tiếng việt Tiếng việt

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học Âm nhạc Âm nhạc

ảnh môn học Công nghệ Công nghệ

ảnh môn học Giáo dục thể chất Giáo dục thể chất

ảnh môn học Hoạt động trải nghiệm Hoạt động trải nghiệm

ảnh môn học Mỹ thuật Mỹ thuật

ảnh môn học Toán học Toán học

ảnh môn học Tin học Tin học

ảnh môn học Tiếng việt Tiếng việt

ảnh môn học HĐ trải nghiệm, hướng nghiệp HĐ trải nghiệm, hướng nghiệp

ảnh môn học Đạo đức Đạo đức

ảnh môn học Âm nhạc Âm nhạc

ảnh môn học Tự nhiên và xã hội Tự nhiên và xã hội

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học Tiếng việt Tiếng việt

ảnh môn học Mỹ thuật Mỹ thuật

ảnh môn học Tự nhiên và xã hội Tự nhiên và xã hội

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học Âm nhạc Âm nhạc

ảnh môn học Toán học Toán học

ảnh môn học Đạo đức Đạo đức

ảnh môn học HĐ trải nghiệm, hướng nghiệp HĐ trải nghiệm, hướng nghiệp

ảnh môn học Toán học Toán học

ảnh môn học Tiếng việt Tiếng việt

ảnh môn học Đạo đức Đạo đức

ảnh môn học Tự nhiên và xã hội Tự nhiên và xã hội

ảnh môn học Tiếng Anh Tiếng Anh

ảnh môn học Sinh học Sinh học
ảnh môn học Tin học Tin học
ảnh môn học Vật lí Vật lí
ảnh môn học Hóa học Hóa học
ảnh môn học Lịch sử Lịch sử
ảnh môn học Công nghệ Công nghệ
ảnh môn học Ngữ văn Ngữ văn
ảnh môn học Toán học Toán học
ảnh môn học GDCD GDCD
ảnh môn học Tiếng Anh Tiếng Anh
ảnh môn học Địa lí Địa lí
Video bài giảng

Bài 5 trang 223 Sách bài tập Hình học lớp 12 Nâng cao.

Lựa chọn câu hỏi để xem giải nhanh hơn
LG a
LG b
LG c

Cho khối lăng trụ tam giác đều ABC.A'B'C' có chiều cao bằng h và hai đường thẳng AB' và BC vuông góc với nhau.

Lựa chọn câu hỏi để xem giải nhanh hơn
LG a
LG b
LG c

LG a

Gọi M' là trung điểm của A'B'. Chứng minh rằng \(AB' \bot BM'.\)

Lời giải chi tiết:

(h.109)

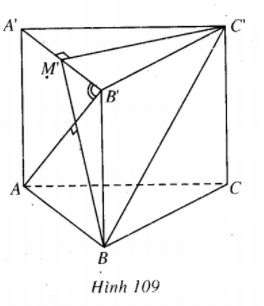
Ta có C'M' \( \bot \) A'B, C'M' \( \bot \) AA' => C'M' \( \bot \) (ABB'A') => C'M' \( \bot \) AB.

Mặt khác, theo giả thiết BC' \( \bot \) AB', suy ra AB' \( \bot \) mp(BC'M').

Do đó AB' \( \bot \) BM'.

LG b

Tính độ dài đoạn thẳng A'B' theo h.

Lời giải chi tiết:

Từ kết quả của câu a), ta dễ dàng suy ra

\(\Delta BB'M'\) đồng dạng \( \Delta B'A'A\)

\(\eqalign{  &  \Rightarrow {{A'B'} \over {BB'}} = {{A'A} \over {B'M'}}  \cr  &  \Rightarrow A'B'.B'M' = A'A.BB'  \cr  &  \Rightarrow {1 \over 2}A'B{'^2} = {h^2}  \cr  &  \Rightarrow A'B' = h\sqrt 2 . \cr} \)

LG c

Tính thể tích khối lăng trụ đã cho.

Lời giải chi tiết:

\({V_{ABC.A'B'C'}} = {S_{A'B'C'}}.AA'\)

                          \(= {\left( {h\sqrt 2 } \right)^2}.{{\sqrt 3 } \over 4}h = {{\sqrt 3 } \over 2}{h^3}.\)

Fqa.vn
Bình chọn:
0/5 (0 đánh giá)
Báo cáo nội dung câu hỏi
Bình luận (0)
Bạn cần đăng nhập để bình luận
Bạn chắc chắn muốn xóa nội dung này ?

Gợi ý sách

Xem thêm
Bạn có câu hỏi cần được giải đáp?

Bộ sách liên quan

FQA.vn Nền tảng kết nối cộng đồng hỗ trợ giải bài tập học sinh trong khối K12. Sản phẩm được phát triển bởi CÔNG TY TNHH CÔNG NGHỆ GIA ĐÌNH (FTECH CO., LTD)
Điện thoại: 1900636019 Email: info@fqa.vn
Location Địa chỉ: Số 21 Ngõ Giếng, Phố Đông Các, Phường Ô Chợ Dừa, Quận Đống Đa, Thành phố Hà Nội, Việt Nam.
Liên kết · Hỏi đáp bài tập · Giải bài tập SGK · Cẩm nang · Đề ôn luyện
hỗ trợ · Điều khoản & chính sách · Sitemap · Liên hệ · Hướng dẫn sử dụng · Đánh giá và góp ý · Dịch vụ FQA media
Tải ứng dụng FQA
Người chịu trách nhiệm quản lý nội dung: Nguyễn Tuấn Quang Giấy phép thiết lập MXH số 07/GP-BTTTT do Bộ Thông tin và Truyền thông cấp ngày 05/01/2024
Copyright © 2023 fqa.vn All Rights Reserved